Thực hành 2 trang 69 SGK Toán 8 Chân trời sáng tạo Tập 2
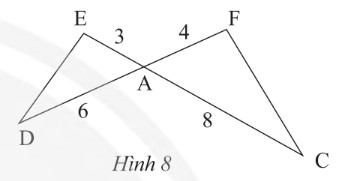
Cho tam giác ADE và tam giác ACF có các kích thước như trong Hình 8.
Chứng minh rằng \(\Delta ADEᔕ\Delta ACF\)?
Hướng dẫn giải chi tiết Thực hành 2
Ta có: \(\frac{AE}{AF}=\frac{3}{4};\frac{AD}{AC}=\frac{6}{8}=\frac{3}{4}\)
Suy ra \(\frac{AE}{AF}=\frac{AD}{AC}\)
Tam giác ADE và ACF có:
- \(\frac{AE}{AF}=\frac{AD}{AC}\) (cmt)
- \(\widehat{DAE}=\widehat{CAF}\) (hai góc đối đỉnh)
Vậy \(\Delta ADEᔕ\Delta ACF\) (c.g.c)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Thực hành 1 trang 68 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Khám phá 2 trang 68 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Khám phá 3 trang 69 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 3 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 1 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 2 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 1 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 2 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 3 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 4 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 5 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 6 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 7 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 8 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 9 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 10 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


