Khám phá 3 trang 69 SGK Toán 8 Chân trời sáng tạo Tập 2
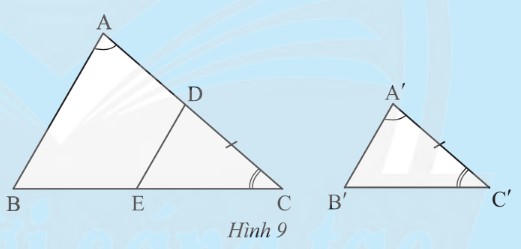
Cho hai tam giác ABC và A'B'C' có \(\widehat{A}=\widehat{A'},\widehat{C}=\widehat{C'}\) (Hình 9).
Trên cạnh AC, Lấy điểm D sao cho DC = A'C'. Qua D kẻ đường thẳng song song với AB cắt cạnh BC tại E.
a) Tam giác DEC có đồng dạng với tam giác ABC không?
b) Nhận xét về mối quan hệ giữa tam giác A'B'C' và tam giác DEC?
c) Dự đoán về sự đồng dạng của hai tam giác A'B'C' và ABC?
Hướng dẫn giải chi tiết Khám phá 3
a) Tam giác ABC có DE // AB nên \(\Delta DECᔕ\Delta ABC\).
b) Ta có: \(\Delta DECᔕ\Delta ABC\), do đó \(\widehat{D}=\widehat{A}\)
Xét tam giác A'B'C' và DEC có:
- \(\widehat{A'}=\widehat{D}\) (cùng \(=\widehat{A}\))
- \(A'C' = DC\) (gt)
- \(\widehat{C'}=\widehat{C}\) (gt)
Suy ra \(\Delta A'B'C' =\Delta DEC\) (g.c.g)
c) Dự đoán: \(\Delta A'B'C'ᔕ\Delta ABC\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Khám phá 2 trang 68 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 2 trang 69 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 3 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 1 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 2 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 1 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 2 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 3 trang 70 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 4 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 5 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 6 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 7 trang 71 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 8 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 9 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 10 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


