Bài tập 9 trang 72 SGK Toán 8 Chân trời sáng tạo Tập 2
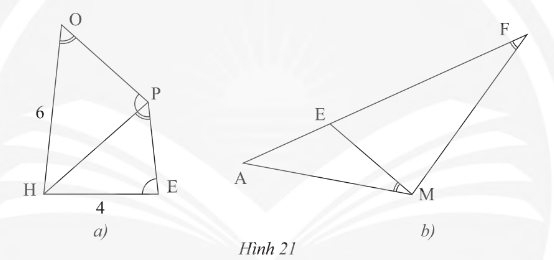
a) Trong Hình 21a, cho biết \(\widehat{HOP}=\widehat{HPE},~\widehat{HPO}=\widehat{HEP},~OH=6~cm\) và \(HE = 4~cm\). Tính độ dài đoạn thẳng HP?
b) Trong Hình 21b, cho biết \(\widehat{AME}=\widehat{AFM}\). Chứng minh rằng \(AM^{2}=AE.AF\)?
Hướng dẫn giải chi tiết Bài 9
a) Xét tam giác HOP và HPE có:
\(\widehat{HOP}=\widehat{HPE},~\widehat{HPO}=\widehat{HEP}\)
Suy ra \(\Delta HOP~ᔕ~\Delta HPE\)
Nên \(\frac{HO}{HP}=\frac{HP}{HE}\)
\(\Rightarrow \frac{6}{HP}=\frac{HP}{4}\)
\(\Rightarrow HP = 2\sqrt{6}\)
b) Xét tam giác AEM và AMF ta có:
- \(\widehat{A}\) chung
- \(\widehat{AME}=\widehat{AFM}\)
\(\Rightarrow \Delta AEM~ᔕ~\Delta AMF\)
Nên \(\frac{AE}{AM}=\frac{AM}{AF}\)
\(\Rightarrow AM^{2}=AE.AF\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





