Giải bài 2.61 tr 132 SBT Toán 12
Giải các bất phương trình sau bằng đồ thị
a) \({\left( {\frac{1}{2}} \right)^x}\)
b) \({\left( {\frac{1}{3}} \right)^x} \ge x + 1\)
c) \({\log _{\frac{1}{3}}}x > 3x\)
d) \({\log _2}x \le 6 - x\)
Hướng dẫn giải chi tiết
a) Vẽ đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) và \(y = x - \frac{1}{2}\) trên cùng một hệ tọa độ ta được:
.png)
Do vậy \({\left( {\frac{1}{2}} \right)^x} < x - \frac{1}{2} \Leftrightarrow x > 1\)
b) Vẽ đồ thị hàm số \(y = {\left( {\frac{1}{3}} \right)^x}\) và trên cùng một hệ tọa độ ta được:
.png)
Từ đồ thị hàm số, ta có: \({\left( {\frac{1}{3}} \right)^x} \ge x + 1 \Rightarrow x \le 0\)
c) Vẽ đồ thị hàm số \(y = {\log _{\frac{1}{3}}}x\) và trên cùng một hệ tọa độ ta được:
.png)
Từ đồ thị hàm số, ta có: \({\log _{\frac{1}{3}}}x > 3x \Rightarrow 0 < x < \frac{1}{3}\)
d) Vẽ đồ thị hàm số \(y = {\log _2}x\) và trên cùng một hệ tọa độ ta được:
.png)
Từ đồ thị hàm số, ta có: \({\log _2}x \le 6 - x \Rightarrow 0 < x \le 4\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
-


Giải bất phương trình mũ sau: \(2^{-x^{2}+3x}< 4\)
bởi Đặng Ngọc Trâm
 01/06/2021
01/06/2021
Giải bất phương trình mũ sau: \(2^{-x^{2}+3x}< 4\)
Theo dõi (0) 1 Trả lời -


Giải bất phương trình: \({\log _{{1 \over 2}}}(2x + 3) > {\log _{{1 \over 2}}}(3x + 1)\,\,\,(1)\).
bởi An Nhiên
 01/06/2021
01/06/2021
Giải bất phương trình: \({\log _{{1 \over 2}}}(2x + 3) > {\log _{{1 \over 2}}}(3x + 1)\,\,\,(1)\).
Theo dõi (0) 1 Trả lời -


Giải bất phương trình sau: \({2^x} + {\rm{ }}{2^{ - x}}-{\rm{ }}3{\rm{ }} < {\rm{ }}0\).
bởi Co Nan
 01/06/2021
01/06/2021
Giải bất phương trình sau: \({2^x} + {\rm{ }}{2^{ - x}}-{\rm{ }}3{\rm{ }} < {\rm{ }}0\).
Theo dõi (0) 1 Trả lời -


Hãy lập bảng tương tự cho các bất phương trình: \({a^x} \ge {\rm{ }}b,{\rm{ }}{a^x} < {\rm{ }}b,{\rm{ }}{a^x} \le {\rm{ }}b\).
bởi Lê Minh Bảo Bảo
 01/06/2021
01/06/2021
Hãy lập bảng tương tự cho các bất phương trình: \({a^x} \ge {\rm{ }}b,{\rm{ }}{a^x} < {\rm{ }}b,{\rm{ }}{a^x} \le {\rm{ }}b\).
Theo dõi (0) 1 Trả lời -
ADMICRO


Giải bất phương trình \({\log _2}\left( {{x^2} - x - 2} \right) \ge 2\)?
bởi Đời'x Khói'snoi'v
 09/06/2020
09/06/2020
Giai bpt: log có so 2 (x^2 - x - 2) > hoac bang 2
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


log3/4 ( 2x-1 )>2
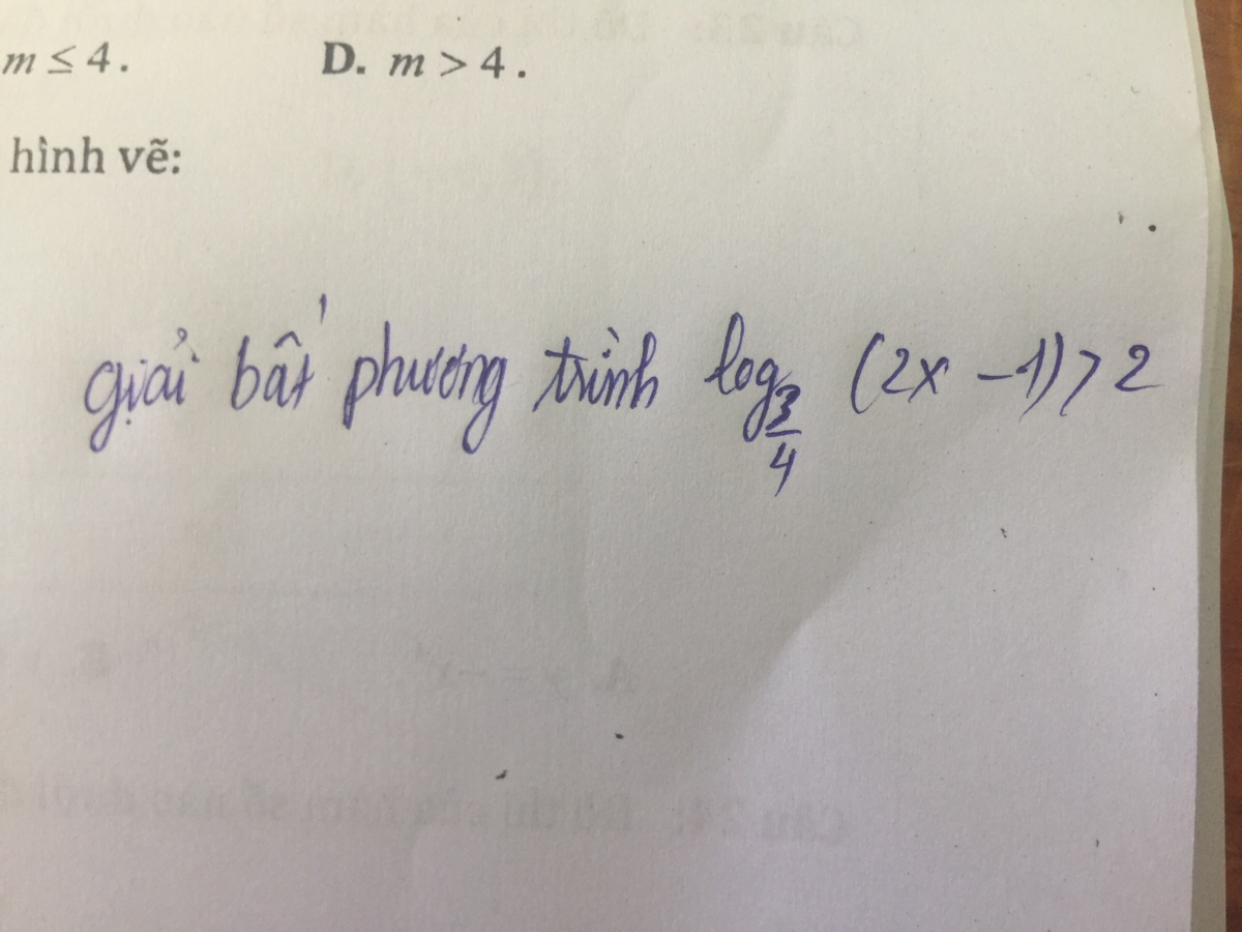 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Số cặp số nguyên dương (m, n) thỏa mãn 1<=m, n<=2018 sao cho 5^m<2^n<2^n+<5^n+1
bởi Trần Hiếu
 14/04/2020
14/04/2020
Có bao nhiêu cặp số nguyên dương (m;n) thoã mãn 1<=m,n<=2018 sao cho 5^m<2^n<2^n+<5^n+1
A.277
B.278
C.279
D.280
Theo dõi (0) 1 Trả lời -


Giải bất phương trình log2 (3x-2)<=6-2x
bởi Tranviet Huy
 09/03/2020
09/03/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Với x thuộc tập hợp nào dưới đây thì không phải là nghiệm của bpt x(5x+2)-x(x^2+6) > 0?
bởi Ha Thai
 12/02/2020
12/02/2020
với x thuộc tập hợp nào dưới đây thì không phải là nghiệm của bpt x(5x+2)-x(x2+6)>0
- A.(-
;1] ∪ [4;+) B.[1;4] C.(1;4) D.[0;1] ∪ [4;+
)
Theo dõi (0) 0 Trả lời - A.(-
-


Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=-x^3+3x-4 trên đoạn (0;2)?
bởi Nhỏ Viên Đá
 10/01/2020
10/01/2020
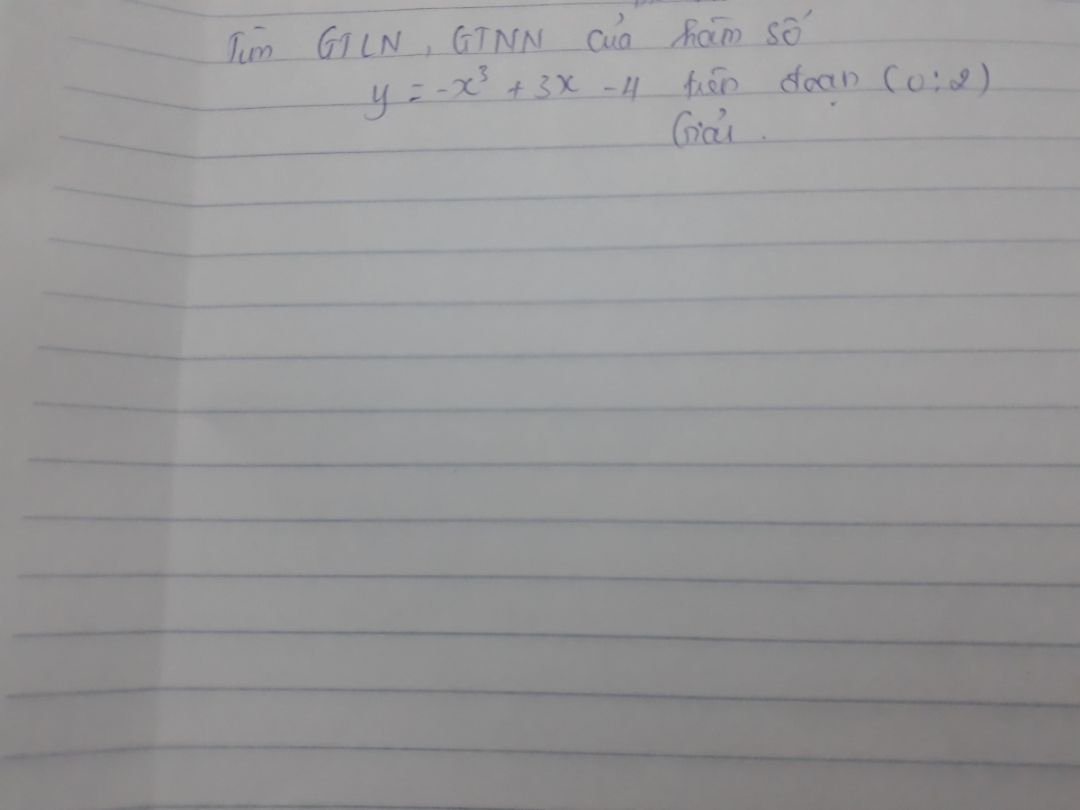 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Giải phương trình (0,5)^(x-2)=2
bởi VT ThẢo
 03/01/2020
03/01/2020
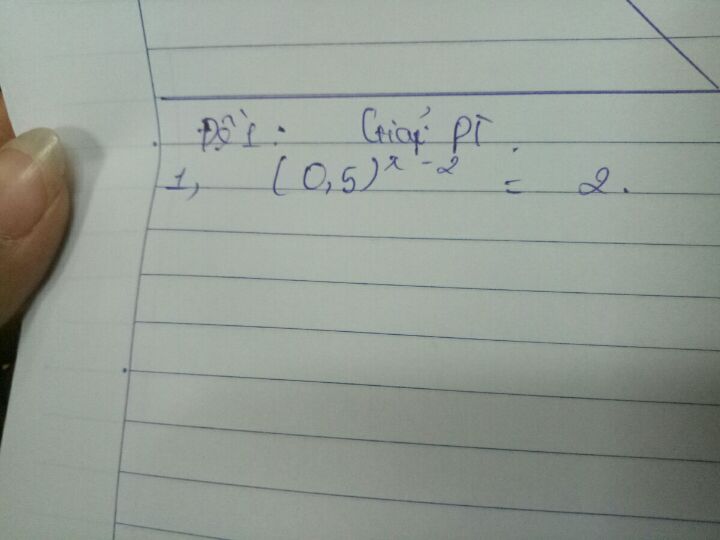 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Có bao nhiêu nghiệm nguyên âm của phương trình log_1/2 (log_6(x^2+x)/(x+4)) > = 0?
bởi Trần Thị TrâmAnh
 30/12/2019
Tìm số nghiệm
30/12/2019
Tìm số nghiệm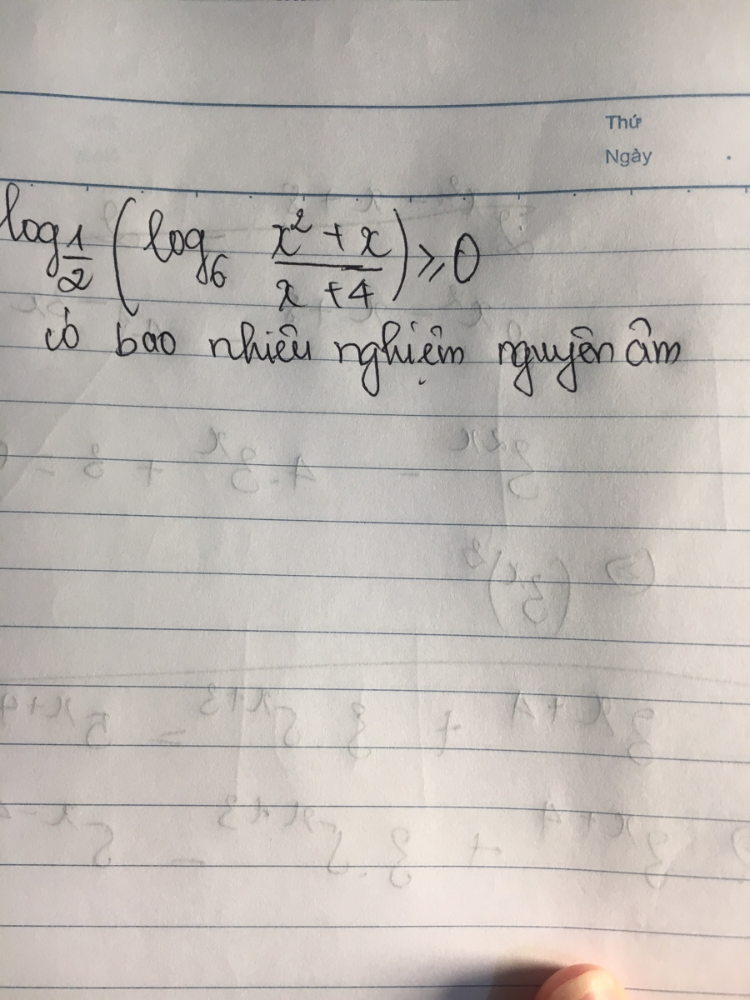 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Phương trình 4^x+2^x(x-7)-4x+12=0 có nghiệm là?
bởi trần thị thảo
 29/12/2019
Mọi người giải giúp em ví dụ 2 với ạ
29/12/2019
Mọi người giải giúp em ví dụ 2 với ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Bất phương trình 2log5x-logx 125>1 có tập nghiệm là?
bởi Phương Thùy
 26/12/2019
Bất phương trình có tập nghiệm là
26/12/2019
Bất phương trình có tập nghiệm là Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để bất phương trình 3^x-(m+3)3^-x-(m+1) > 0 nghiệm đúng với mọi x thuộc R
bởi DT Thanh Thủy
 24/12/2019
Tìm tham số m
24/12/2019
Tìm tham số m Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -

 ghgggghfdvvTheo dõi (0) 0 Trả lời
ghgggghfdvvTheo dõi (0) 0 Trả lời -


Giải bất phương trình x+log_0,2(1-5^x) > = 0
bởi vầy thị ơn
 23/12/2019
Giải bất phương trình
23/12/2019
Giải bất phương trình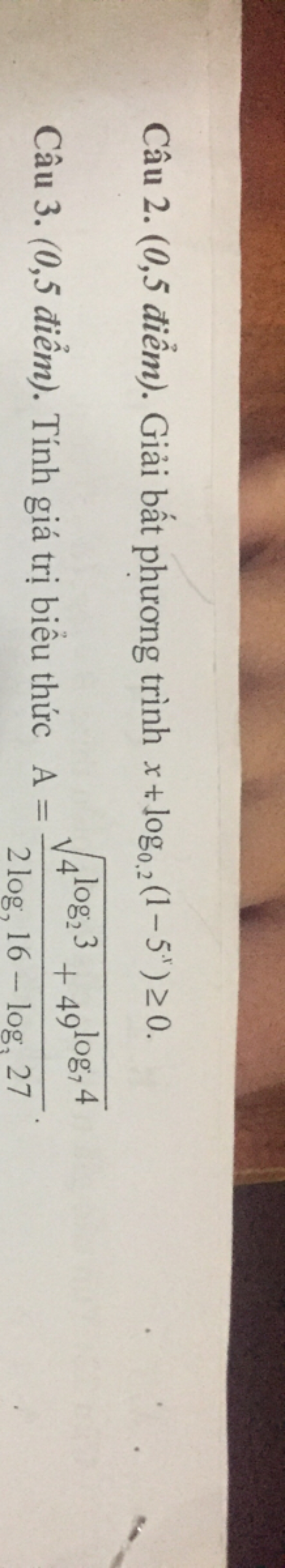 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời





