Giải bài 1.49 tr 24 SBT Toán 12
a) Cho hàm số \(y = \frac{{3 - x}}{{x + 1}}\) có đồ thị H (H.1.1)
Chỉ ra một phép biến hình biến (H) thành (H') có tiệm cận ngang và tiệm cận đứng .
b) Lấy đối xứng (H') qua gốc O, ta được hình (H''). Viết phương trình của (H'').
Hướng dẫn giải chi tiết
a)Từ đồ thị (H) (H.1.1), để có hình (H’) nhận là tiệm cận ngang và là tiệm cận đứng, ta tịnh tiến đồ thị (H) song song với trục Oy lên trên 3 đơn vị, sau đó tịnh tiến song song với trục Ox về bên phải 3 đơn vị, ta được các hàm số tương đường sau:
\(\begin{array}{l}
y = f\left( x \right) = \frac{{3 - x}}{{x + 1}} + 3 = \frac{{3 - x + 3x + 3}}{{x + 1}} = \frac{{2x + 6}}{{x + 1}}\\
y = g\left( x \right) = \frac{{2\left( {x - 3} \right) + 6}}{{x - 3 + 1}} = \frac{{2x}}{{x - 2}}\,\,\,\left( {H'} \right)
\end{array}\)
b) Lấy đối xứng hình (H’) qua gốc O, ta được hình (H’’) có phương trình là
\(y = h\left( x \right) = - \frac{{ - 2\left( { - x} \right)}}{{\left( { - x} \right) - 2}} = - \frac{{ - 2x}}{{ - 2 - x}} = - \frac{{2x}}{{x + 2}}\)
-- Mod Toán 12 HỌC247
Bài tập SGK khác
-


Tìm các tiệm cận của đồ thị hàm số sau: \(y=\dfrac{7}{x}-1\).
Theo dõi (0) 1 Trả lời -


Tìm các tiệm cận của đồ thị hàm số sau: \(y=\dfrac{2x-5}{5x-2}\).
Theo dõi (0) 1 Trả lời -


Cho biết đường thẳng \({\rm{x}} = 1\) là tiệm cận đứng của đồ thị hàm số nào dưới đây?
bởi Anh Nguyễn
 07/05/2021
07/05/2021
A. \(y = \frac{{x - 1}}{{{x^2} + 1}}\)
B. \(y = \sqrt {{x^2} - 1} \)
C. \(y = \frac{{{x^2} - 1}}{{x - 1}}\)
D. \(\frac{1}{{{x^2} - 1}}\)
Theo dõi (0) 1 Trả lời -


Tìm tất cả các giá trị thực của tham sồ m để đồ thị hàm số y=mx^3 -2/x^2-3x+2 có 2 đường tiệm cận đứng
bởi Gia Bảo
 06/09/2020
06/09/2020
tìm tất cả các giá trị thực của tham sồ m để đồ thị hàm số y=mx^3 -2/x^2-3x+2 có 2 đường tiệm cận đứng
Theo dõi (0) 0 Trả lời -
ADMICRO


Với giá trị nào của m thì đồ thị hàm số \(y={x+5 \over x^2+6x+m}\) có ba đường tiệm cận?
bởi miumiu
 02/09/2020
02/09/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Đồ thị hàm số \(y={2x \over x^2+ 1}\) có bao nhiêu đường tiệm cận đứng?
bởi bùi thị phương thơm
 02/09/2020
02/09/2020
Số đường tiệm cận đứng của đồ thị hàm số \(y={2x \over x^2+ 1}\)?
Theo dõi (0) 5 Trả lời -


Tìm đường tiệm cận của đồ thị sau \(y = \frac{{\sqrt x + 1}}{{\sqrt x - 1}}\)?
bởi Do Bang
 17/08/2020
Theo dõi (0) 4 Trả lời
17/08/2020
Theo dõi (0) 4 Trả lời -


Hàm số y=f(x) có bao nhiêu tiệm cận?
bởi Hải Trường
 09/08/2020
09/08/2020
Câu 9
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


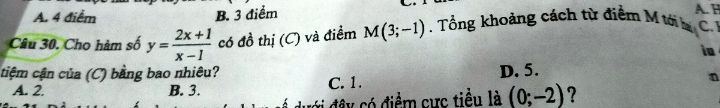 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tiệm cân đứng và tiệm cận ngang của các hàm số sau:
bởi Phạm Bình
 04/08/2020
04/08/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -

 Tìm phương trình đường tiệm cận của đồ thị hàm số y=(1-x)/(1 x)Theo dõi (0) 5 Trả lời
Tìm phương trình đường tiệm cận của đồ thị hàm số y=(1-x)/(1 x)Theo dõi (0) 5 Trả lời -


Với giá trị m nào thì tiệm cận ngang của đồ thị hàm số y =(mx 1):(x-m) đi qua điểm A(1 ‚- 2)
bởi Võ Như Ý Nhi
 19/05/2020
Với giá trị m nào thì tiệm cận ngang của đồ thị hàm số y =(mx 1):(x-m) đi qua điểm A (1 ‚- 2)Theo dõi (0) 1 Trả lời
19/05/2020
Với giá trị m nào thì tiệm cận ngang của đồ thị hàm số y =(mx 1):(x-m) đi qua điểm A (1 ‚- 2)Theo dõi (0) 1 Trả lời -


Có bao nhiêu điểm M thuộc C có tung độ là số nguyên dương sao cho khoảng cách từ m đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị F?
bởi Bich Linh
 30/04/2020
Cho hàm số y=(2x 1):(x-1) có đồ thị C .Có bao nhiêu điểm M thuộc C có tung độ là số nguyên dương sao cho khoảng cách từ m đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị FTheo dõi (0) 0 Trả lời
30/04/2020
Cho hàm số y=(2x 1):(x-1) có đồ thị C .Có bao nhiêu điểm M thuộc C có tung độ là số nguyên dương sao cho khoảng cách từ m đến tiệm cận đứng bằng 3 lần khoảng cách từ M đến tiệm cận ngang của đồ thị FTheo dõi (0) 0 Trả lời -


Tổng tất cả các giá trị của tham số m để đồ thị hàm số y=(x+1)/(x^2-2x+m) có đúng hai đường tiệm cận.
bởi Như Trần
 29/03/2020
giải hộ mình câu này với, tại mình thấy do bậc tử lớn hơn mẫu nên có 1 tiệm cận ngang y=0 rồi, mà còn TCĐ thì mình k làm đc
29/03/2020
giải hộ mình câu này với, tại mình thấy do bậc tử lớn hơn mẫu nên có 1 tiệm cận ngang y=0 rồi, mà còn TCĐ thì mình k làm đc Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Bnm
Bnm Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm số đường tiệm cận của hàm số y=(7x-2)/(x^2-4)
bởi LÊ THỊ LOAN
 18/02/2020
18/02/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Giúp em trả lời những câu hỏi :> cám ơn ạ.
Giúp em trả lời những câu hỏi :> cám ơn ạ. Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Tìm m thuộc C để khoảng cách tiệm cận đứng tiệm cận ngangTheo dõi (0) 0 Trả lời
Tìm m thuộc C để khoảng cách tiệm cận đứng tiệm cận ngangTheo dõi (0) 0 Trả lời -


Tìm m để đường thẳng d: y=-x+m giao với đồ thị hàm số y=(2x+1)/(x+1) tại 2 điểm phân biệt A, B
bởi Nguyễn Tâm
 02/01/2020
A hay d ạ
02/01/2020
A hay d ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Số đường tiệm cận của hàm số y=x+2/x-2
bởi Cong Hung
 27/12/2019
27/12/2019
 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -

 Đáp án chinhTheo dõi (0) 4 Trả lời
Đáp án chinhTheo dõi (0) 4 Trả lời -


Số các giá trị của tham số m để đồ thị hàm số y=(x+m)/(mx+1) không có tiệm cận đứng?
bởi Trinh Cam
 17/12/2019
.
17/12/2019
.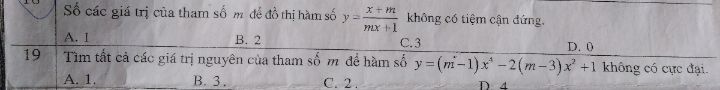 Theo dõi (1) 5 Trả lời
Theo dõi (1) 5 Trả lời






