Bài tập 49 trang 48 SGK Toán 11 NC
Giải phương trình:
\(\frac{{1 + \cos 2x}}{{\cos x}} = \frac{{\sin 2x}}{{1 - \cos 2x}}\)
Hướng dẫn giải chi tiết
ĐKXĐ: \(\cos x \ne 0\) và \(\cos 2x \ne 1\). Với điều kiện đó, ta có:
\(\begin{array}{*{20}{l}}
{\frac{{1 + \cos 2x}}{{\cos x}} = \frac{{\sin 2x}}{{1 - \cos 2x}}}\\
{ \Leftrightarrow \frac{{2{{\cos }^2}x}}{{\cos x}} = \frac{{2\sin x\cos x}}{{2{{\sin }^2}x}}}\\
{ \Leftrightarrow 1 - \frac{1}{{2\sin x}} = 0}\\
\begin{array}{l}
\Leftrightarrow \sin x = \frac{1}{2}\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{6} + k2\pi {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( n \right)}\\
{x = \frac{{5\pi }}{6} + k2\pi {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( n \right)}
\end{array}} \right.\left( {k \in Z} \right)
\end{array}
\end{array}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 47 trang 48 SGK Toán 11 NC
Bài tập 48 trang 48 SGK Toán 11 NC
Bài tập 50 trang 48 SGK Toán 11 NC
Bài tập 51 trang 48 SGK Toán 11 NC
Bài tập 52 trang 48 SGK Toán 11 NC
Bài tập 53 trang 49 SGK Toán 11 NC
Bài tập 54 trang 49 SGK Toán 11 NC
Bài tập 55 trang 49 SBT Toán 11 NC
Bài tập 56 trang 49 SGK Toán 11 NC
Bài tập 57 trang 49 SGK Toán 11 NC
Bài tập 58 trang 49 SGK Toán 11 NC
Bài tập 59 trang 49 SGK Toán 11 NC
Bài tập 60 trang 49 SGK Toán 11 NC
Bài tập 61 trang 49 SGK Toán 11 NC
-


Giải phương trình cos^2 3x.cos2x sin^2x=0
bởi Hồng Thắm
 12/12/2019
cos^23x×cos2x sin^2x=0
12/12/2019
cos^23x×cos2x sin^2x=0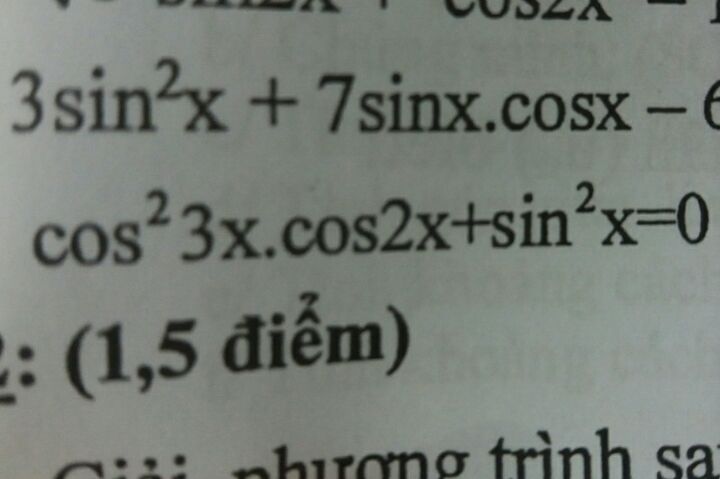 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm điều kiện và giải phương trình (1-2sinx-sin2x+2cosx)/(2sinx-1)=cos2x-căn 3(1+cos2x)
bởi Thúy Hằng
 06/12/2019
06/12/2019
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Giải phương trình sin3x-cos3x=1
bởi Bùi Thảo My
 06/12/2019
Giải các phương trìnhTheo dõi (0) 0 Trả lời
06/12/2019
Giải các phương trìnhTheo dõi (0) 0 Trả lời -


Giải phương trình 2sinx=-căn 3 với x thuộc (0;2pi)
bởi kẹo
 01/12/2019
...
01/12/2019
... Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Giải phương trình 1+cos2x+cos4x =0
bởi Kim Phượng
 29/11/2019
29/11/2019
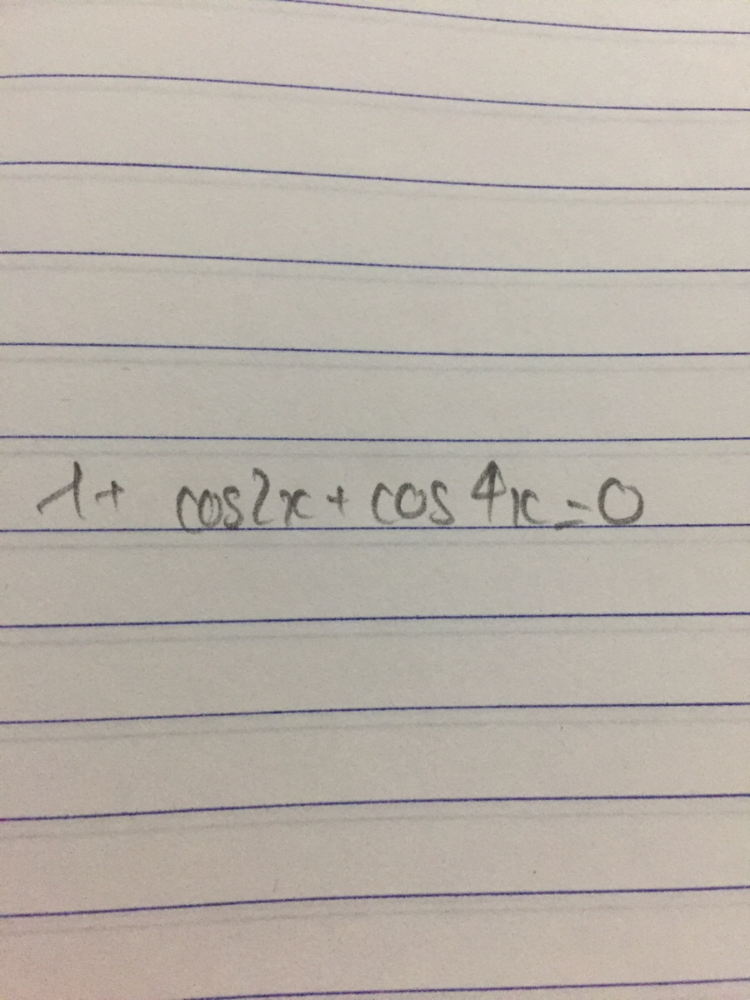 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Đề cương học kì 1 môn Toán 11 năm học 2019 - 2020
bởi Kim Kim
 28/11/2019
Đề cương học kì cho bạn nào cần, nếu có thể thì hãy giải ra và bình luận nhé, cảm ơn
28/11/2019
Đề cương học kì cho bạn nào cần, nếu có thể thì hãy giải ra và bình luận nhé, cảm ơn Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm ảnh của A, đường thẳng d, đường tròn (C) qua phép đồng dạng có được từ việc thực hiện liên tiếp phép vị tự tâm O tỉ số 2 và phép tịnh tiến theo vectơ v =(2,-2)
bởi Ều Ều
 06/11/2019
06/11/2019
Tìm ảnh của A, đường thẳng d, đường tròn (C) qua phép đồng dạng có được từ việc thực hiện liên tiếp phép vị tự tâm O tỉ số 2 và phép tịnh tiến theo vectơ v =(2,-2)
Theo dõi (0) 3 Trả lời -


Tìm GTNN của hàm số y=1-2cosx+cos^2x
bởi Linh
 22/10/2019
22/10/2019
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình sin(2x-pi/5)=sin(pi/5+x)
bởi Thucky Duong
 21/10/2019
Sin(2x-pi/5)=sin(pi/5 x)
21/10/2019
Sin(2x-pi/5)=sin(pi/5 x) Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời





