Bài tập 48 trang 48 SGK Toán 11 NC
a. Chứng minh rằng \(\sin \frac{\pi }{{12}} = \frac{{\sqrt 3 - 1}}{{2\sqrt 2 }}\)
b. Giải các phương trình \(2\sin x - 2\cos x = 1 - \sqrt 3 \) bằng cách biến đổi vế trái về dạng Csin(x+α)
c. Giải phương trình \(2\sin x - 2\cos x = 1 - \sqrt 3 \) bằng cách bình phương hai vế.
Hướng dẫn giải chi tiết
a) Ta có:
\(\begin{array}{l}
\sin \frac{\pi }{{12}} = \sin \left( {\frac{\pi }{3} - \frac{\pi }{4}} \right)\\
= \sin \frac{\pi }{3}\cos \frac{\pi }{4} - \sin \frac{\pi }{4}\cos \frac{\pi }{3}\\
= \frac{{\sqrt 3 }}{2}.\frac{{\sqrt 2 }}{2} - \frac{{\sqrt 2 }}{2}.\frac{1}{2}\\
= \frac{{\sqrt 6 - \sqrt 2 }}{4} = \frac{{\sqrt 2 \left( {\sqrt 3 - 1} \right)}}{4} = \frac{{\sqrt 3 - 1}}{{2\sqrt 2 }}
\end{array}\)
b) Ta có:
\(\begin{array}{l}
2\sin x - 2\cos x = 1 - \sqrt 3 \\
\Leftrightarrow \frac{1}{{\sqrt 2 }}\sin x - \frac{1}{{\sqrt 2 }}\cos x = \frac{{1 - \sqrt 3 }}{{2\sqrt 2 }}\\
\Leftrightarrow \sin x.\cos \frac{\pi }{4} - \sin \frac{\pi }{4}\cos x = - \sin \frac{\pi }{{12}}\\
\Leftrightarrow \sin \left( {x - \frac{\pi }{4}} \right) = \sin \left( { - \frac{\pi }{{12}}} \right)\\
\Leftrightarrow \left[ \begin{array}{l}
x - \frac{\pi }{4} = - \frac{\pi }{{12}} + k2\pi \\
x - \frac{\pi }{4} = \pi + \frac{\pi }{{12}} + k2\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{6} + k2\pi \\
x = \frac{{4\pi }}{3} + k2\pi
\end{array} \right.\left( {k \in Z} \right)
\end{array}\)
c) Chú ý rằng \(1 - \sqrt 3 < 0\), ta đặt điều kiện sinx–cosx < 0 rồi bình phương hai vế của phương trình thì được:
\(\begin{array}{l}
4\left( {1 - \sin 2x} \right) = 4 - 2\sqrt 3 \\
\Leftrightarrow \sin 2x = \frac{{\sqrt 3 }}{2} \Leftrightarrow \left[ \begin{array}{l}
x = \frac{\pi }{6} + k\pi \\
x = \frac{\pi }{3} + k\pi
\end{array} \right.\left( {k \in Z} \right)
\end{array}\)
Thử vào điều kiện sinx–cosx < 0, ta thấy:
- Họ nghiệm \(x = \frac{\pi }{6} + k\pi \) thỏa mãn điều kiện sinx–cosx < 0 khi và chỉ khi k chẵn, tức là \(x = \frac{\pi }{6} + 2m\pi ,m \in Z\).
- Họ nghiệm \(x = \frac{\pi }{3} + k\pi \) thỏa mãn điều kiện sinx–cosx < 0 khi và chỉ khi k lẻ, tức là \(x = \frac{\pi }{3} + k\pi \).
Ta có kết quả như đã nêu ở câu b.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 46 trang 48 SGK Toán 11 NC
Bài tập 47 trang 48 SGK Toán 11 NC
Bài tập 49 trang 48 SGK Toán 11 NC
Bài tập 50 trang 48 SGK Toán 11 NC
Bài tập 51 trang 48 SGK Toán 11 NC
Bài tập 52 trang 48 SGK Toán 11 NC
Bài tập 53 trang 49 SGK Toán 11 NC
Bài tập 54 trang 49 SGK Toán 11 NC
Bài tập 55 trang 49 SBT Toán 11 NC
Bài tập 56 trang 49 SGK Toán 11 NC
Bài tập 57 trang 49 SGK Toán 11 NC
Bài tập 58 trang 49 SGK Toán 11 NC
Bài tập 59 trang 49 SGK Toán 11 NC
Bài tập 60 trang 49 SGK Toán 11 NC
Bài tập 61 trang 49 SGK Toán 11 NC
-


Giải phương trình cosx=3sinx+1
bởi Phạm Văn Quang
 19/12/2019
19/12/2019
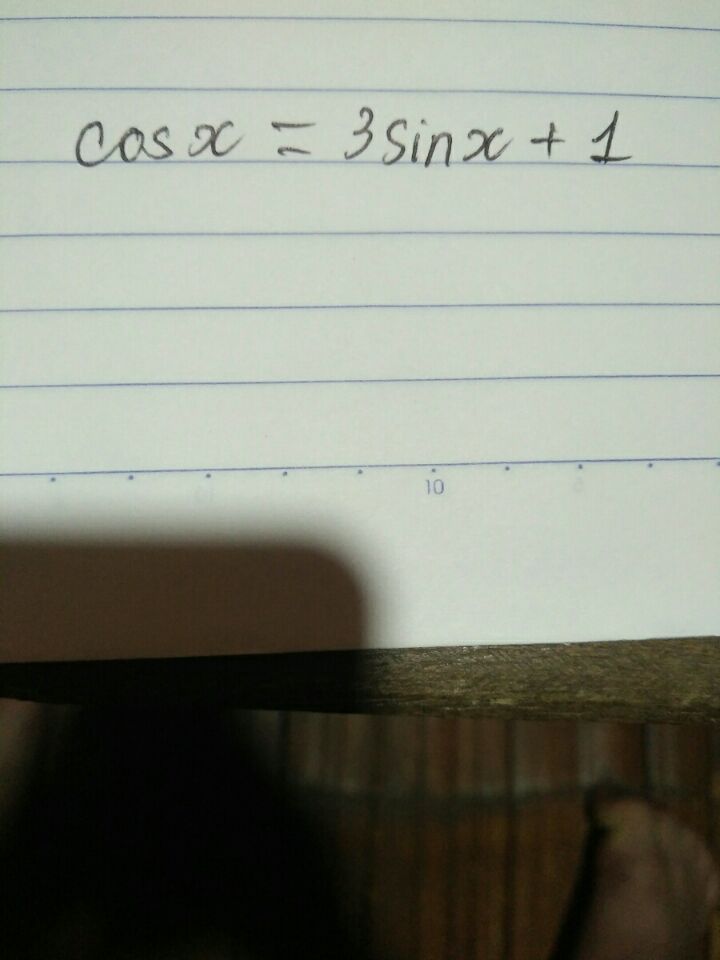 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 2 câu này luôn ạ
2 câu này luôn ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Có bao nhiêu giá trị nguyên của m để phương trình đã cho có đúng 1 nghiệm trên [0;2pi/3]?
bởi Ngọc Trinh
 16/12/2019
16/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Có bao nhiêu giá trị nguyên m thuộc (-2019;2019) để hàm số xác định với mọi giá trị của x?
bởi Trung Hiếu
 16/12/2019
16/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Tìm m để bất phương trình sau nghiệm đúng với mọi x thuộc R
bởi NQ
 15/12/2019
15/12/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình lượng giác 2cos^ x+cos2x=2
bởi Ly Khánh
 15/12/2019
a) 2cos bình x cos2x=2
15/12/2019
a) 2cos bình x cos2x=2 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Chu kì của hàm số y=cos x là?
bởi Liên Ngọc
 13/12/2019
13/12/2019
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm gtln, gtnn của biểu thức f(x)= sin^3x cos^3x
bởi Nguyễn Ngân
 12/12/2019
Em cần gấp ạ. Cảm ơn trướcTheo dõi (0) 2 Trả lời
12/12/2019
Em cần gấp ạ. Cảm ơn trướcTheo dõi (0) 2 Trả lời -


Tìm m để phương trình msin2x +căn 3cos2x=m +1
bởi Uyên Phương
 12/12/2019
tìm m để phương trình msin2x √3cos2x=m 1Theo dõi (0) 3 Trả lời
12/12/2019
tìm m để phương trình msin2x √3cos2x=m 1Theo dõi (0) 3 Trả lời





