Bài tập 38 trang 71 SBT Toán 9 Tập 1
Cho các hàm số:
y = 2x – 2 (d1)
y = - (4/3).x – 2 (d2)
y = (1/3).x + 3 (d3)
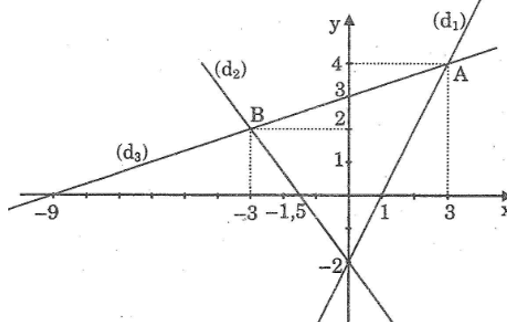
a. Vẽ đồ thị các hàm số đã cho trên cùng một mặt phẳng tọa độ.
b. Gọi giao điểm của đường thẳng (d3) với (d1) và (d2) theo thứ tự là A và B. Tìm tọa độ của A, B.
c. Tính khoảng cách AB.
Hướng dẫn giải chi tiết
a. *Vẽ đồ thị hàm số y = 2x – 2 (d1)
Cho x = 0 thì y = -2. Ta có: (0; -2)
Cho y = 0 thì 2x – 2 = 0 ⇔ 2x = 2 ⇔ x = 1. Ta có: (1; 0)
Đồ thị hàm số đi qua hai điểm (0; -2) và (1; 0)
*Vẽ đồ thị hàm số y = - (4/3).x – 2 (d2)
Cho x = 0 thì y = -2. Ta có: (0; -2)
Cho y = 0 thì - (4/3).x – 2 = 0 ⇔ x = -1,5. Ta có: (-1,5; 0)
Đồ thị hàm số đi qua hai điểm (0; -2) và (-1,5; 0)
*Vẽ đồ thị hàm số y = (1/3).x + 3 (d3)
Cho x = 0 thì y = 3. Ta có: (0; 3)
Cho y = 0 thì (1/3).x + 3 = 0 ⇔ x = -9. Ta có: (-9; 0)
Đồ thị hàm số đi qua hai điểm (0; 3) và (-9; 0)
b. Phương trình hoành độ giao điểm của (d1) và (d3):
2x – 2 = (1/3).x + 3 ⇔ 2x - (1/3).x = 3 + 2 ⇔ (5/3).x = 5 ⇔ x = 3
Tung độ giao điểm: y = 2.3 – 2 ⇔ y = 6 – 2 = 4
Vậy tọa độ điểm A là A(3; 4)
Phương trình hoành độ giao điểm của (d2) và (d3):
- (4/3).x – 2 = (1/3).x + 3 ⇔ (1/3).x + (4/3).x = -2 – 3 ⇔ (5/3).x = -5 ⇔ x = -3
Tung độ giao điểm: y = (1/3).(-3) + 3 ⇔ y = -1 + 3 = 2
Vậy tọa độ điểm B là B(-3; 2)
c. Ta có: AB2 = (xA – xB)2 + (yA – yB)2 = (3 + 3)2 + (4 – 2)2 = 40
AB = √40 = 2√10 .
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 36 trang 70 SBT Toán 9 Tập 1
Bài tập 37 trang 71 SBT Toán 9 Tập 1
Câu hỏi 1 trang 59 SGK Toán 9 Tập 1
Câu hỏi 2 trang 60 SGK Toán 9 Tập 1
Câu hỏi 32 trang 61 SGK Toán 9 Tập 1
Câu hỏi 33 trang 61 SGK Toán 9 Tập 1
Câu hỏi 34 trang 61 SGK Toán 9 Tập 1
Câu hỏi 35 trang 61 SGK Toán 9 Tập 1
Câu hỏi 36 trang 61 SGK Toán 9 Tập 1
-


Chứng minh rằng x^2/a^2 +y^2/b^2 + z^2/c^2=1
bởi Anh Trần
 16/01/2019
16/01/2019
Cho \(\dfrac{x}{a}+\dfrac{y}{b}+\dfrac{z}{c}=1\)và \(\dfrac{a}{x}+\dfrac{b}{y}+\dfrac{c}{z}=0\). Chứng minh rằng: \(\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1\)
Theo dõi (0) 1 Trả lời -


Tính nhanh giá trị biểu thức A=(50^2+48^2+46^2+...+4^2+2^2)-(49^2-47^2+45^2+..+5^2+3^2+1^2)
bởi Chai Chai
 16/01/2019
16/01/2019
Tính nhanh giá trị biểu thức: \(A=\left(50^2+48^2+46^2+...+4^2+2^2\right)-\left(49^2+47^2+45^2+...+5^2+3^2+1^2\right)\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng với mọi giá trị dương của a,b ta đều có (1 + a + b ) ( ab + a + b ) ≥ 9
bởi hoàng duy
 16/01/2019
16/01/2019
CMR:Với mọi GT dương của a,b ta đều có:
( 1 + a + b ) ( ab + a + b ) \(\ge\) 9
Theo dõi (0) 1 Trả lời -


Chứng minh rằng x^2-y^2 chia hết cho 40
bởi Sam sung
 16/01/2019
16/01/2019
Với x,y nguyên thỏa mãn \(\dfrac{x^2-1}{2}=\dfrac{y^2-1}{3}\) chứng minh rằng x^2-y^2 chia hết cho 40
Các bạn giúp mình với. Mình cảm ơn nhiều!Theo dõi (0) 1 Trả lời -
ADMICRO


Cho các số thực dương X,Y,Z.c/m: \(\dfrac{X^2}{Y+Z}\)+\(\dfrac{Y^2}{Z+X}\)+\(\dfrac{Z^2}{X+Y}\)\(\ge\)\(\dfrac{X+Y+Z}{2}\)
Theo dõi (0) 1 Trả lời -


1.Giả sử n là số nguyên dương thỏa mãn điều kiện n2+n+3 là số nguyên tố.Cmr n:3 dư 1 và 7n2+6n+2017 không phải số chính phương
2.Tìm số tự nhiên n lớn nhất để số 431+42018+4n là số chính phương
3.Cho n là một số tự nhiên sao cho \(\dfrac{n^2-1}{3}\) là tích của hai số tự nhiên liên tiếp.Cmr n là tổng của hai số chính phương liên tiếp
Theo dõi (0) 1 Trả lời -


Giải phương trình nghiêm nguyên 3⋅x^2−4⋅y^2=13
bởi Nguyễn Hiền
 28/01/2019
28/01/2019
Giải phương trình nghiêm nguyên:
\(3\cdot x^2-4\cdot y^2=13\)
Theo dõi (0) 1 Trả lời -


Xác định hàm số y=ax+b song song với đường thẳng y=-2+3 và đi qua điểm B (3 ; 1)
bởi Trần Thị Trang
 29/10/2018
29/10/2018
xác định hàm số y=ax+b
a) biết đồ thị của hàm số song song với đường thẳng y=-2+3 và đi qua điểm B ( 3 ; 1 ).
b) vẽ đồ thị của hàm số vừa tìm được ở câu a .
Theo dõi (0) 1 Trả lời -


Chứng minh rằng ad+b+c=bc+a+d
bởi Thu Hang
 16/01/2019
16/01/2019
Cho a,b,c khác d, thõa mãn \(ac-a-c=b^2-2b,bd-b-d=c^2-2c\)
C/m : \(ad+b+c=bc+a+d\)
Theo dõi (0) 1 Trả lời -


Cho các số dương x,y,z thỏa mãn \(x^3+y^3+z^3=1\). CMR :
\(\dfrac{x^2}{\sqrt{1-x^2}}+\dfrac{y^2}{\sqrt{1-y^2}}+\dfrac{z^2}{\sqrt{1-z^2}}\ge2\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng a/(b-c)^2 + b/(c-a)^2+c/(a-b)^2=0
bởi Hoàng My
 16/01/2019
16/01/2019
Cho 3 số thực a,b,c thõa : \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{a+b+c}\)
C/m : \(\dfrac{a}{\left(b-c\right)^2}+\dfrac{b}{\left(c-a\right)^2}+\dfrac{c}{\left(a-b\right)^2}=0.\)
Cm bài toán tổng quát :
giả sử a,b,c là các số thực thõa mãn \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=\dfrac{1}{a+b+c}.\)
C/M : \(\dfrac{1}{a^n}+\dfrac{1}{b^n}+\dfrac{1}{c^n}=\dfrac{1}{a^n+b^n+c^n}\forall n\in N.\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng 1/x^2+1 + 1/y^2+1 + 1/z^2+1 >=3/2
bởi con cai
 16/01/2019
16/01/2019
cho x,y,z>0 thỏa mãn xyz=1. chứng minh rằng 1/x²+1 + 1/y²+1 + 1/z²+1 >=3/2
Theo dõi (0) 1 Trả lời -


Xác định hàm số y=ax+b cắt trục tung có tung độ bằng -3 và đi qua điểm A (2, -2)
bởi thu phương
 29/10/2018
29/10/2018
xác định hàm số y=ax+b
a) biết đồ thị hàm số cắt trục tung có tung độ bằng -3 và đi qua điểm A ( 2 : -2 ).
b) vẽ đồ thị của hàm số vừa tìm được ở câu a.
Theo dõi (0) 1 Trả lời -


cho ba số thực dương a, b, c thỏa mãn ab + bc + ca = 3. Chứng minh rằng: \(\dfrac{a^3}{b^2+3}+\dfrac{b^3}{c^2+3}+\dfrac{c^3}{a^3+3}\ge\dfrac{3}{4}\) help me!!!!
Theo dõi (0) 1 Trả lời -


Tính giá trị biểu thức M = x^2007 + y^2007
bởi Phan Thị Trinh
 16/01/2019
16/01/2019
Cho x,y thỏa mãn \(\left(\sqrt{x^2+2007}+x\right)\left(\sqrt{y^2+2007}+y\right)=2007\)
Tính giá trị biểu thức \(M=x^{2007}+y^{2007}\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng 0
bởi Tra xanh
 16/01/2019
16/01/2019
Cho các số thực a,b,c đồng thời thỏa mãn:
\(a< b< c;a+b+c=6;ab+bc+ca=9\)
CMR: \(0< a< 1< b< 3< c< 4\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng HC=2.ON
bởi Nguyễn Lê Thảo Trang
 16/01/2019
16/01/2019
Cho tam giác ABC nhọn có góc BAC=45 độ . Hai đường cao BD và CE cắt nhau ở H. Gọi I là trung điểm của DE. Kẻ EM vuông góc với AC, DN vuông góc với AB. O là giao điểm của EM và DN.
a/ Chứng minh rằng HC=2.ON
b/ HI đi qua trọng tâm tam giác ABC.
Các bạn ới giúp mk với
Theo dõi (0) 1 Trả lời -


Chứng minh rằng (a+b+1/4)^2 + (b+c+1/4)^2 + (c+a+1/4)^2 >= 4(1/1/a+1/b + 1/1/b+1/c + 1/1/c+1/a)
bởi Nguyễn Anh Hưng
 16/01/2019
16/01/2019
cho a,b,c>0, CMR:
\(\left(a+b+\dfrac{1}{4}\right)^2+\left(b+c+\dfrac{1}{4}\right)^2+\left(c+a+\dfrac{1}{4}\right)^2\ge4\left(\dfrac{1}{\dfrac{1}{a}+\dfrac{1}{b}}+\dfrac{1}{\dfrac{1}{b}+\dfrac{1}{c}}+\dfrac{1}{\dfrac{1}{c}+\dfrac{1}{a}}\right)\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng a^7 + 3b^7 − 2c chia hết cho 7
bởi thi trang
 16/01/2019
16/01/2019
Cho các số nguyên a, b, c khác ) thoả mãn điều kiện : \(\dfrac{5b+2c\left(4+c^6\right)}{a+b+c}=1.\) Chứng minh rằng: \(a^7+3b^7-2c\) chia hết cho 7.
Theo dõi (0) 1 Trả lời -


Chứng minh rằng 1/a^4(b+c)^2 >=3/4
bởi ngọc trang
 16/01/2019
16/01/2019
cho \(a,b,c>0\),\(abc=1\)
chứng minh rằng:
\(\sum\dfrac{1}{a^4\left(b+c\right)^2}\ge\dfrac{3}{4}\)
Theo dõi (0) 1 Trả lời -


Chứng minh M=a^5_1+a^5_2+a^5_3+...+a^5_2017
bởi Thuy Kim
 16/01/2019
16/01/2019
Cho các số nguyên dương: \(a_1;a_2;a_3;...;a_{2017}\)sao cho :
\(N=a_1+a_2+a_3+...+a_{2017}\)chia hết cho 30.
Chứng minh: \(M=a^5_1+a^5_2+a^5_3+...+a^5_{2017}\)chia hết cho 30.
Theo dõi (0) 1 Trả lời -


Chứng minh rằng HA/BC+HB/CA+HC/AB >= căn3
bởi Hoa Lan
 16/01/2019
16/01/2019
Cho tam giác ABC có ba góc nhọn và H là trực tâm. CMR
\(\dfrac{HA}{BC}+\dfrac{HB}{CA}+\dfrac{HC}{AB}\)≥\(\sqrt{3}\)
Theo dõi (1) 1 Trả lời -


Chứng minh rằng ( 2^147 − 1 ) ⋮ 343
bởi Mai Trang
 16/01/2019
16/01/2019
Chứng minh rằng: \(\left(2^{147}-1\right)⋮343\)
Theo dõi (0) 1 Trả lời -


Chứng minh rằng nếu n>3 thì tích ab chia hết cho 6 với a, b, n là số nguyên dương và b<10
bởi Trần Thị Trang
 16/01/2019
16/01/2019
Cho \(2^n=10a+b\). Chứng minh rằng nếu n>3 thì tích ab chia hết cho 6 với a, b, n là số nguyên dương và b<10
Theo dõi (0) 1 Trả lời -


Chứng minh rằng với mọi số nguyên n thì n^2 + 11n + 39 không chia hết cho 49
bởi minh vương
 16/01/2019
16/01/2019
Chứng minh rằng với mọi số nguyên n thì \(n^2+11n+39\) không chia hết cho 49.
Theo dõi (0) 1 Trả lời -


Cho 4 số nguyên a, b, c, d. Chứng minh rằng: (b-a)(c-a)(d-a)(d-c)(d-b)(c-b) chia hết cho 12.
Theo dõi (0) 1 Trả lời -


Chô a,b,c là các số đôi một khác nhau.CMR:
\(\sqrt{\dfrac{1}{\left(a-b\right)^2}+\dfrac{1}{\left(b-c\right)^2}-\dfrac{1}{\left(c-a\right)^2}}\)là một số hữu tỉ
Theo dõi (0) 1 Trả lời -


Chứng minh rằng A = p^8n + 23p^4n + 16 chia hết cho 5
bởi Nguyen Ngoc
 16/01/2019
16/01/2019
Cho p là số nguyên tố lớn hơn 5. Chứng minh rằng: \(A=p^{8n}+23p^{4n}+16\) chia hết cho 5.
Theo dõi (0) 1 Trả lời -


Chứng minh nếu \(\sqrt{x^2+\sqrt[3]{x^4y^2}}+\sqrt{y^2+\sqrt[3]{x^2y^4}}=a\) thì \(\sqrt[3]{x^2}+\sqrt[3]{y^2}=\sqrt[3]{a^2}\)
Theo dõi (0) 1 Trả lời