Bài tập 20 tr 102 sách BT Toán lớp 9 Tập 2
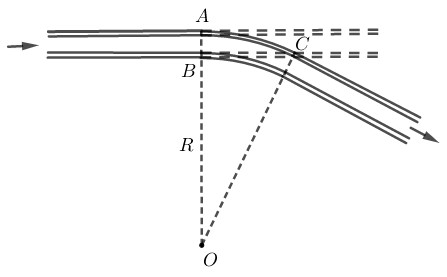
Để giúp xe lửa chuyển từ một đường ray từ hướng này sang một đường ray theo hướng khác, người ta làm xen giữa một đoạn đường ray hình vòng cung (hình \(1\)). Biết chiều rộng của đường ray là \(AB \approx 1,1m\), đoạn \(BC \approx 28,4m\). Hãy tính bán kính \(OA = R\) của đoạn đường ray hình vòng cung.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
Ta xem hai đoạn đường ray thẳng là tiếp tuyến của hai đoạn đường ray vòng cung.
Điểm \(B\) cố định nằm trong đường tròn có cung \(\overparen{AC}\).
Đường thẳng \(OB\) cắt đường tròn đó tại \(A\) và \(A’.\)
\(A\) cố định và \(A’\) cố định
\(B\) là tiếp điểm cung nhỏ trong nên \(BC\) là tiếp tuyến của đường tròn \((O; OB)\)
\( \Rightarrow BC \bot OB\). Kéo dài \(BC\) cắt đường tròn \((O; OA)\) tại \(C’\)
\( \Rightarrow BC = BC'\) (đường kính vuông góc dây cung)
Xét \(∆BAC\) và \(∆BA'C:\)
+) \(\widehat {ABC} = \widehat {C'BA'}\) (đối đỉnh)
+) \(\widehat {ACB} = \widehat {C'A'B}\) (\(2\) góc nội tiếp cùng chắn cung \(\overparen{AC'}\))
Suy ra: \(∆BAC\) đồng dạng \(∆BC'A' \;\;(g.g)\)
\( \Rightarrow \displaystyle {{BC'} \over {AB}} = {{BA'} \over {BC}}\)
\( \Rightarrow BC.BC' = AB.BA'\) mà \(BC = BC’; BA’ = 2R – AB\)
Suy ra: \(B{C^2} = AB\left( {2R - AB} \right)\)
\({\left( {28,4} \right)^2} \approx 1,1.\left( {2R - 1,1} \right)\)
\( \Rightarrow 2,2R \approx 806,56 + 1,21\)
\(R \approx 807,77:2,2 = 367,2\) \((m).\)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Cho tam giác ABC nội tiếp đường tròn (O), biết góc AOB=140 độ, góc BOC=80 độ. Tính các góc tam giác ABC.
bởi The Hao Ly
 12/01/2020
12/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Chứng minh Bx//MN biết tia tiếp tuyến Bx của đường tròn ngoại tiếp tứ giác ANMC
bởi Mai Tram
 09/04/2019
09/04/2019
Cho tam giác ABC nhọn nội tiếp đường tròn tâm O, đường cao AM, CN.
a) chứng minh tứ giác ANMC nội tiếp. Xác định tâm của đường tròn.
b) chứng minh góc MAC = góc MNC
c) Kẻ tia tiếp tuyến Bx của đường tròn ngoại tiếp tứ giác ANMC. Chứng minh Bx // MN
Theo dõi (2) 1 Trả lời





