Bài tập 21 tr 102 sách BT Toán lớp 9 Tập 2
Cho tam giác \(ABC\) nội tiếp trong đường tròn tâm \(O,\) biết \(\widehat A = {32^0}\), \(\widehat B = {84^0}\). Lấy các điểm \(D, E, F\) thuộc đường tròn tâm \(O\) sao cho \(AD = AB,\) \(BE = BC,\) \(CF = CA.\) Hãy tính các góc của tam giác \(DEF.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của cung bị chắn.
Lời giải chi tiết
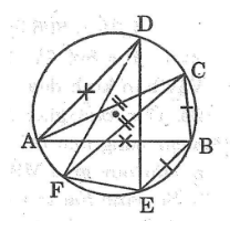
Xét đường tròn \((O)\) có:
\(\widehat A =\displaystyle {1 \over 2} sđ \overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow sđ \overparen{BC}\) \( = 2\widehat A = {2.32^o} = {64^o}\)
Ta có: \(BC = BE \;\;(gt)\)
\( \Rightarrow sđ \overparen{BC}\)\( = sđ \overparen{BE}= 64^o\)
Mà \(\widehat B = \displaystyle {1 \over 2} sđ \overparen{AC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AC}\) \( = 2\widehat B = {2.84^o} = {168^o}\)
Lại có: \(AC = CF \;\;(gt)\)
\( \Rightarrow sđ \overparen{CF}\) \(= sđ \overparen{AC}= 168^o\)
\( sđ \overparen{AC} + sđ \overparen{AF} + sđ \overparen{CF}\)\( = 360^o\)
\( \Rightarrow sđ \overparen{AF}\) \( = {360^o} - sđ \overparen{AC} - sđ \overparen{CF}\)\( = 360^o – 168^o. 2 = 24^o\)
Trong \(∆ABC\) ta có: \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat A + \widehat B} \right)\)
\( = {180^0} - \left( {{{32}^o} + {{84}^o}} \right) = {64^o}\)
Mà \( \widehat {ACB} = \displaystyle {1 \over 2} sđ \overparen{AB}\) (tính chất góc nội tiếp)
\( \Rightarrow sđ \overparen{AB} = 2\widehat {ACB} = {2.64^o} = {128^o}\)
Lại có \(AD = AB\;\; (gt)\)
\( \Rightarrow sđ \overparen{AD} = sđ \overparen{AB} = 128^o\)
Ta có: \(\widehat {FED} = \displaystyle {1 \over 2} sđ \overparen{DF}\) \( =\displaystyle {1 \over 2} ( sđ \overparen{AD} + sđ \overparen{AF}\))
\(= \displaystyle{1 \over 2}.\left( {{{128}^o} + {{24}^o}} \right) = {76^o}\)
\(\widehat {EDF} = \displaystyle{1 \over 2} sđ \overparen{EF}\) \(=\displaystyle {1 \over 2} ( sđ \overparen{AB} - sđ \overparen{AF} - sđ \overparen{BE})\)
\(= \displaystyle{1 \over 2}.\left( {{{128}^o} - {{24}^o} - {{64}^o}} \right) = {20^o}\)
\(\widehat {DFE} = {180^o} - \left( {\widehat {FED} + \widehat {EDF}} \right)\)
\(= {180^0} - \left( {{{76}^o} + {{20}^o}} \right) = {84^o}\).
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Chứng minh rằng ba điểm H,M,F thẳng hàng
bởi thanh hằng
 25/01/2019
25/01/2019
Cho tam giác ABC nội tiếp đường tròn (O), hai đường cao BD và CE cắt nhau tại H. Vẽ đường kính AF.
a) Tứ giác BFCH là hình gì?
b) Gọi M là trung điểm của BC. Chứng minh rằng ba điểm H,M,F thẳng hàng
c) Chứng minh rằng Om=1/2AH
Theo dõi (0) 1 Trả lời -


Bài 22 trang 102 sách bài tập toán 9 tập 2
bởi Nguyễn Quang Thanh Tú
 10/10/2018
Bài 22 (Sách bài tập - tập 2 - trang 102)
10/10/2018
Bài 22 (Sách bài tập - tập 2 - trang 102)Vẽ một tam giác vuông biết cạnh huyền là 4cm và đường cao ứng với cạnh huyền là 1,5cm ?
Theo dõi (0) 1 Trả lời -


Bài 21 trang 76 SGK Toán 9 tập 1
bởi Hoa Lan
 21/02/2019
Bài 21 (SGK trang 76)
21/02/2019
Bài 21 (SGK trang 76)Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì? Tại sao?
Theo dõi (0) 1 Trả lời





