Bài tập 20 tr 102 sách BT Toán lớp 9 Tập 2
Cho tam giác đều \(ABC\) nội tiếp đường tròn \((O)\) và \(M\) là một điểm của cung nhỏ \(BC.\) Trên \(MA\) lấy điểm \(D\) sao cho \(MD = MB.\)
\(a)\) Hỏi tam giác MBD là tam giác gì\(?\)
\(b)\) So sánh hai tam giác \(BDA\) và \(BMC.\)
\(c)\) Chứng minh rằng \(MA = MB + MC.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Ta sử dụng kiến thức:
+) Trong một đường tròn, hai góc nội tiếp cùng chắn một cung thì bằng nhau.
Lời giải chi tiết
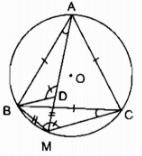
a) MB = MD (gt) \( \Rightarrow \) ∆MBD cân tại M
\(\widehat {AMB} = \widehat {ACB}\) (2 góc nội tiếp cùng chắn cung \(\overparen{AB}\))
Mà \(\widehat {ACB} = {60^0}\) (vì ∆ABC đều)
\( \Rightarrow \widehat {AMB} = {60^0}\) hay \(\widehat {DMB} = {60^0}\)
Vậy ∆MBD đều
b) ∆MBD đều
\( \Rightarrow \widehat {DBC} + \widehat {CBM} = \widehat {DBM} = {60^0}\) (1)
∆ABC đều \( \Rightarrow \widehat {ABD} + \widehat {DBC} = \widehat {ABC} = {60^0}\) (2)
Từ (1) và (2) suy ra: \(\widehat {CBM} = \widehat {ABD}\)
Xét ∆BDA và ∆BMC:
BA = BC (gt)
\(\widehat {ABD} = \widehat {CBM}\) (chứng minh trên)
BD = BM (vì ∆MBD đều)
Suy ra: ∆BDA = ∆BMC (c.g.c)
c) ∆BDA = ∆BMC (chứng minh trên)
\( \Rightarrow DA = MC\)
Ta có: MB = MD (gt) mà AM = AD + DM
Suy ra: MA = MD + MC.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Chứng minh tam giác DBE cân
bởi cuc trang
 22/01/2019
22/01/2019
Δ ABC cân tại A \(\left(\widehat{A}=90^o\right)\). Vẽ đường tròn đường kính AB cắt \(\stackrel\frown{BC}\) tại D, cắt \(\stackrel\frown{AC}\) tại E. Chứng minh:
a) \(\Delta DBE\) cân
b) \(\widehat{CBE}=\dfrac{1}{2}\widehat{BAC}\)
Theo dõi (0) 1 Trả lời -


Chứng minh AP là tia phân giác của góc OAH
bởi Phạm Khánh Ngọc
 22/01/2019
22/01/2019
Cho tam giác ABC nội tiếp đường tròn,đường phân giác của góc A cắt đường tròn ở P, đường cao AH cắt cạnh BC ở H.Cm a) OP // AH b) AP là tia phân giác của góc OAH
Theo dõi (0) 1 Trả lời -


Chứng minh BC là tia phân giác của góc HBE
bởi Nguyễn Thị Trang
 22/01/2019
22/01/2019
Cho tam giác ABC nội tiếp đường tròn O và trực tâm H nằm trong tam giác. Tia AH cắt BC ở I, cắt đường tròn O ở E. Chứng minh:
a) BC là tia phân giác của góc HBE
b) H và E đối xứng với nhau qua BC
Theo dõi (0) 1 Trả lời





