Bài tập 16 trang 64 SBT Toán 9 Tập 1
Cho hàm số y = (a – 1)x + a
a. Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2.
b. Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -3.
c. Vẽ đồ thị của hai hàm số ứng với giá trị của a tìm được ở các câu a, b trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
Hướng dẫn giải chi tiết
a. Hàm số y = (a – 1)x + a (a ≠ 1) là hàm số bậc nhất có đồ thị hàm số cắt trục tung tại điểm có tung độ bằng y = 2 nên a = 2.
b. Hàm số y = (a – 1)x + a (a ≠ 1) là hàm số bậc nhất có đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = -3 nên tung độ giao điểm này bằng 0.
Ta có: 0 = (a – 1)(-3) + a ⇔ -3x + 3 + a = 0
⇔ -2a = -3 ⇔ a = 1,5
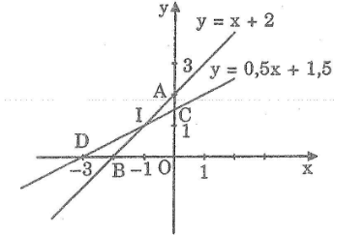
c. Khi a = 2 thì ta có hàm số: y = x + 2
Khi a = 1,5 thì ta có hàm số: y = 0,5x + 1,5
*Vẽ đồ thị của hàm số y = x + 2
Cho x = 0 thì y = 2. Ta có: A(0; 2)
Cho y = 0 thì x = -2. Ta có: B(-2; 0)
Đường thẳng AB là đồ thị hàm số y = x + 2
*Vẽ đồ thị hàm số y = 0,5x + 1,5
Cho x = 0 thì y = 1,5. Ta có: C(0; 1,5)
Cho y = 0 thì x = -3. Ta có: D(-3; 0)
Đường thẳng CD là đồ thị hàm số y = 0,5x + 1,5.
*Tọa độ giao điểm của hai đường thẳng:
Gọi I(x1; y1) là tọa độ giao điểm của hai đường thẳng.
Ta có: I thuộc đường thẳng y = x + 2 nên y1 = x1 + 2
I thuộc đường thẳng y = 0,5x + 1,5 nên y1 = 0,5x1 + 1,5
Suy ra: x1 + 2 = 0,5x1 + 1,5 ⇔ 0,5x1= -0,5 ⇔ x1 = -1
x1 = -1 ⇒ y1 = -1 + 2 = 1
Vậy tọa độ giao điểm của hai đường thẳng là I(-1; 1)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Vẽ đồ thị hàm số y=2x
bởi Tường Vy
 07/11/2019
07/11/2019
 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


cho hàm số y = mx - 3, xác định m trong mỗi trường hợp sau:
a, đồ thị hàm số song song với đường thẳng y = -3x
b, khi x = 1 + √3thì y = √3
Theo dõi (0) 2 Trả lời -


Tìm m để (d1) và (d2) cắt nhau biết (d1) : mx - y =1, (d2) : 2x + y =3
bởi Đào Mai Phương
 03/02/2019
03/02/2019
Cho 2 đường thẳng (d1) : mx - y =1 ; (d2) : 2x + y =3
a, Tìm m để (d1) và (d2) cắt nhau
b, Tìm m để (d1) cắt (d2) tại A (x;y) sao cho x>0 ; y>0
Theo dõi (0) 1 Trả lời -


Lập PT đi qua điểm A(2;-1) và B(-1;5)
Theo dõi (0) 1 Trả lời -
ADMICRO


Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số y = -2x, y = 0,5x
bởi ミ★Bạch Kudo★彡
 20/01/2019
20/01/2019
a. Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm sô:
y = -2x (1)
y = 0,5x (2)
b. Qua điểm K(0; 2) vẽ đường thẳng (d) song song với trục Ox. Đường thẳng (d) cắt các đường thẳng (1) và (2) lần lượt tại A và B. Tìm tọa độ của các điểm A, B.
c. Hãy chứng tỏ rằng góc (AOB) = 90o (hai đường thẳng y = -2x và y = 0,5x vuông góc với nhau).
Theo dõi (0) 1 Trả lời -


Xác định giá trị của a để đồ thị của hàm số y = (a – 1)x + a cắt trục tung
bởi ミ★Bạch Kudo★彡
 20/01/2019
20/01/2019
Cho hàm số y = (a – 1)x + a
a. Xác định giá trị của a để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng 2.
b. Xác định giá trị của a để đồ thị của hàm số cắt trục hoành tại điểm có hoành độ bằng -3.
c. Vẽ đồ thị của hai hàm số ứng với giá trị của a tìm được ở các câu a, b trên cùng hệ trục tọa độ Oxy và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
Theo dõi (0) 1 Trả lời -


Cho hàm số y = (m – 3)x
a. Với giá trị nào của m thì hàm số đồng biến? Nghịch biến?
b. Xác định giá trị của m để đồ thị của hàm số đi qua điểm A(1; 2)
c. Xác định giá trị của m để đồ thị của hàm số đi qua điểm B(1; -2)
d. Vẽ đồ thị của hai hàm số ứng với giá trị của m tìm được ở các câu b, c.
Theo dõi (0) 0 Trả lời -


Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số y = x (d1), y = 2x (d2)
bởi ミ★Bạch Kudo★彡
 20/01/2019
20/01/2019
a. Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau đây:
y = x (d1)
y = 2x (d2)
y = -x + 3 (d3)
b. Đường thẳng (d3) cắt đường thẳng (d1) và (d2) theo thứ tự tại A, B. Tìm tọa độ của các điểm A, B.
Theo dõi (0) 0 Trả lời -


Tìm nghiệm nguyên của 40x + 31y = 1
bởi Nguyễn Hoàng Ngân
 04/01/2019
04/01/2019
Tìm nghiệm nguyên của 40x + 31y = 1
( Nếu chép trên mạng nhớ giải thích rõ )Theo dõi (0) 0 Trả lời -


Cho hai đường thẳng (d1): y=12x+5-m; (d2): y=3x+3+m. Xác định m để giao điểm của (d1) và (d2) thỏa mãn
a) Nằm trên trục tung
b) Nằm bên trái trục tung
c) Nằm trong góc phần tư thứ ha
Theo dõi (1) 5 Trả lời -


Xác định a ,b biết đồ thị hàm số đi qua A(2;-1) và cắt trục hoành tại điểm B
bởi phan thị thu hà
 14/12/2018
14/12/2018
Cho hàm số y=ax+b
a) Xác định a ,b biết đồ thị hàm số đi qua A(2;-1) và cắt trục hoành tại điểm B có hoành độ bằng
b) Vẽ đồ thị hàm số vừa xác định a ,b ?
Theo dõi (0) 1 Trả lời -


Tìm m thuộc Z để đường thẳng y=2x-m^2-3 cắt đường thẳng y=x-4 tại 1 điểm
bởi Trần Tuấn Anh
 03/12/2018
03/12/2018
Tìm m ∈ Z để đường thẳng y= 2x-
-3. Cắt đường thẳng y= x-4 tại một điểm nằm trong góc phần tư thứ IV?
Theo dõi (0) 2 Trả lời -


Tìm m để y =(m-2)x+m là hàm số bậc nhất
bởi Bình Nguyen
 26/10/2018
26/10/2018
Cho hàm số y =(m-2)x+m (d)
a) Tìm m để hàm số đã cho là hàm số bậc nhất .
b) Tìm m để hàm số đồng biến .
c) Tìm m để hàm số nghịch biến .
d) Tìm m để (d) cắt trục tung tại điểm có tung độ là 2.
e) Tìm m để (d) cắt trục hoành tại điểm có hoành độ là -3 .
f) Vẽ d với m=-1
Theo dõi (0) 1 Trả lời -


Cho (d) là đồ thị hàm số của 2(m-1)x + (m-2)y = 2. Chứng minh rằng:
a/ (d) luôn đi qua một điểm cố định với mọi m.
b/ Tìm m để (d) cách gốc toạ độ một khoảng lớn nhất.
Theo dõi (1) 1 Trả lời -


Giải hệ phương trình mx+y=3, 4x+my=6 khi m=1
bởi Ngoc Nga
 07/01/2019
07/01/2019
Cho hpt : mx+y=3
4x+my=6
a) giải hệ khi m=1
b) tìm m để hpt có nghiệm duy nhất (x;y) sao cho x,y nguyên dương
Theo dõi (0) 1 Trả lời -


Cho hpt :\(\int_{x+2y=3m+2}^{3x-y=2m-1}\)
Tìm m để hệ phương trình trên có nghiệm duy nhất (x;y) thoả mãn :
x2 + y2 =10
Theo dõi (0) 1 Trả lời