Bài tập 14 trang 64 SBT Toán 9 Tập 1
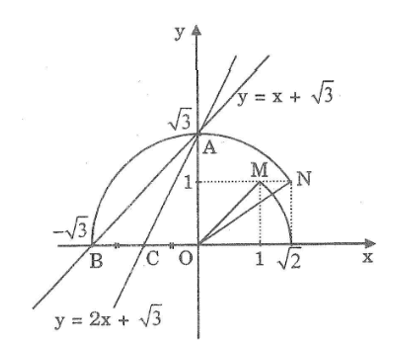
a. Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ:
y = x + \(\sqrt 3 \) (1)
y = 2x + \(\sqrt 3 \) (2)
b. Gọi giao điểm của đường thẳng y = x + \(\sqrt 3 \) với các trục Ox, Oy theo thứ tự là A, B và giao điểm của đường thẳng y = 2x + \(\sqrt 3 \) với các trục Ox, Oy theo thứ tự là A, C. Tính các góc của tam giác ABC.
Hướng dẫn giải chi tiết
a. *Vẽ đồ thị của hàm số y = x + \(\sqrt 3 \)
Cho x = 0 thì y = \(\sqrt 3 \) . Ta có: A(0; √3 )
Cho y = 0 thì x + \(\sqrt 3 \) = 0 => x = - √3 . Ta có: B(-\(\sqrt 3 \) ; 0)
Cách tìm điểm có tung độ bằng √3 trên trục Oy:
- Dựng điểm M(1; 1). Ta có: OM = √2
- Dựng cung tròn tâm O bán kính OM cắt trục OX tại điểm có hoành độ bằng 2
- Dựng điểm N(1; \(\sqrt 2 \) ). Ta có: ON = √3
- Vẽ cung tròn tâm O bán kính ON cắt trục Oy tại A có tung độ 3 cắt tia đối của Ox tại B có hoành độ -3
Đồ thị của hàm số y = x + \(\sqrt 3 \) là đường thẳng AB.
*Vẽ đồ thị của hàm số y = 2x + \(\sqrt 3 \)
Cho x = 0 thì y = \(\sqrt 3 \) . Ta có: A(0; \(\sqrt 3 \) )
Cho y = 0 thì 2x + \(\sqrt 3 \) = 0 => x = - √3/2 . Ta có: C(-√3/2 ; 0)
Đồ thị của hàm số y = 2x + √3 là đường thẳng AC.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Tìm tọa độ giao điểm của (P) và (d)?
bởi Ma Vương
 02/05/2020
Giải phần b khó quá
02/05/2020
Giải phần b khó quá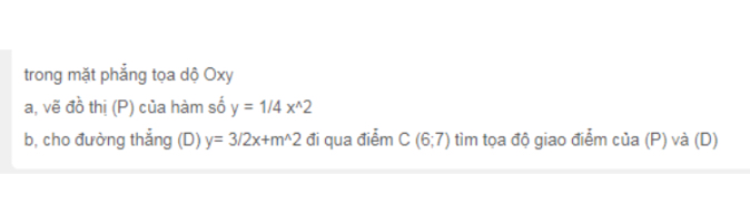 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chọn đáp án đúng?
bởi Nguyên Tuân
 22/04/2020
22/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tìm m để đồ thị hàm số y=(m-1)x+26 đi qua điểm A(1;-2)
bởi Huyền Lê
 22/04/2020
22/04/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Cho hàm số y = ax^2. Tìm hệ số a biết đồ thị hàm số đi qua M(1;2)
Theo dõi (0) 2 Trả lời -


Chứng minh khi m thay đổi (d) luôn đi qua 1 điểm cố định
bởi Anh Nhat
 18/04/2020
Cho đường thẳng (d): y=mx-m 1 và Parabol (P): y= x^2 a. Chứng minh khi m thay đổi (d) luôn đi qua 1 điểm cố định. b. Tìm m để (d) cắt (P) tại hai điểm phân biệt nằm ở bên phải trục tung. c. Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn: |x1| |x2|=5Theo dõi (0) 0 Trả lời
18/04/2020
Cho đường thẳng (d): y=mx-m 1 và Parabol (P): y= x^2 a. Chứng minh khi m thay đổi (d) luôn đi qua 1 điểm cố định. b. Tìm m để (d) cắt (P) tại hai điểm phân biệt nằm ở bên phải trục tung. c. Tìm m để (d) cắt (P) tại hai điểm phân biệt có hoành độ x1, x2 thỏa mãn: |x1| |x2|=5Theo dõi (0) 0 Trả lời -


viết phương trình đường thẳng đi qua góc tạo độ O và điểm M(2,4)
a.viết phương trình dạng parabol dạng y =ax^2 và đi qua điểm M(2,4)
b.Vẽ parabol và đường thẳng trên trong cùng một hệ trục toạ độ và tìm toạ độ của chúng
Theo dõi (0) 0 Trả lời -

 Giải hộ mình vs ạTheo dõi (1) 4 Trả lời
Giải hộ mình vs ạTheo dõi (1) 4 Trả lời -


Vẽ đồ thị hàm số y=0,4x
bởi Nguyễn Sơn
 04/04/2020
04/04/2020
 Theo dõi (0) 10 Trả lời
Theo dõi (0) 10 Trả lời -


Tìm tọa độ giao điểm của hai hàm số y=-2x và y=x+5
bởi Sara Naluin
 03/04/2020
03/04/2020
 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Vẽ đồ thị của hàm số sau trên cùng mặt phẳng toạ độ (d1): y=x-3, (d2): y=-x-1.
bởi Hoàng Lệ
 03/04/2020
a, Vẽ đồ thị của hàm số sau trên cùng mặt phẳng toạ độ (d1):y=x-3,'(d2)y=-x-1.b, (d1)cắt Ox tại A:(d2) cắt Ox tại B, '(d1)và (d2) cắt nhau tại C. Tính số đo góc của tam giác ABC (Làm tròn đến độ ).c, tính diện tích của tam giác ABC
03/04/2020
a, Vẽ đồ thị của hàm số sau trên cùng mặt phẳng toạ độ (d1):y=x-3,'(d2)y=-x-1.b, (d1)cắt Ox tại A:(d2) cắt Ox tại B, '(d1)và (d2) cắt nhau tại C. Tính số đo góc của tam giác ABC (Làm tròn đến độ ).c, tính diện tích của tam giác ABC Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Cho hàm số y=(m-1)x+m+1 (m là tham số) có đò thị là d. Tìm m để d song song với đường thẳng y=2x+1.
bởi wennjaa
 03/04/2020
03/04/2020
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Giúp em với
Giúp em với Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Vẽ đồ thị hàm số d1:y=2x-3 và tìm d2 biết d2//d1 và d2 đi qua điểm M tọa độ là M=(1;8)
bởi Decade Through
 23/03/2020
23/03/2020
cho đường thẳng d1:y=2x-3
1)vẽ đồ thị hàm số d1
2)Tìm đường thẳng d2 biết d2//d1 và d2 đi qua điểm M tọa độ là M=(1;8)
Theo dõi (0) 0 Trả lời -


Trong cùng mặt phẳng tọa độ Oxy, vẽ đồ thị hai hàm số y=2x+1 (d) và y=-2x+1 (d'), tìm toajddooj giao điểm của (d) và (d') bằng phép tính.
bởi nguyễn thị minh anh
 19/03/2020
19/03/2020
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Cho hàm số y=(5-3m)x+2 a) Vẽ đồ thị hàm số khi m=1 b) Tìm m để đò thị hầm số tạo với dương trục OX góc 135 độ.
bởi Decade Through
 18/03/2020
18/03/2020
cho hàm số y=(5-3m)*x+2
a.vẽ đồ thị hàm số khi m=1
b.tìm m để đò thị hầm số tạo với dương trục OX góc 135độ
Theo dõi (0) 3 Trả lời