Bài tập 15 trang 102 SBT Toán 9 Tập 2

Hướng dẫn giải

+) Vẽ hình: dùng thước thẳng và compa để vẽ hình

+) Chứng minh: Sử dụng dấu hiệu nhận biết hình bình hành và hình vuông

Dấu hiệu nhận biết hình bình hành: Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành.

Dấu hiệu nhận biết hình chữ nhật: Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật. 

Dấu hiệu nhận biết hình vuông: Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.

Lời giải chi tiết

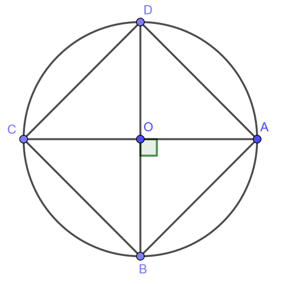
Cách vẽ: 

- Vẽ đường tròn \((O; 1,5cm)\)

- Vẽ 2 đường kính \(AC\) và \(BD\) vuông góc với nhau.

- Nối \(AB, BC, CD, DA\) ta có tứ giác \(ABCD\) là hình vuông có \(4\) đỉnh nằm trên cung tròn \((O; 1,5cm)\).

Chứng minh:

Theo cách vẽ ta có: \(OA = OC=R, OB = OD=R\) nên tứ giác \(ABCD\) là hình bình hành

Lại có: \(AC = BD=2R\) nên hình bình hành \(ABCD\) là hình chữ nhật.

Mặt khác: \(BD \bot AC\) nên hình chữ nhật \(ABCD\) là hình vuông.

Vậy tứ giác \(ABCD\) là hình vuông.

-- Mod Toán 9 HỌC247