Bài tập 16 trang 102 SBT Toán 9 Tập 2

Hướng dẫn giải

Ta sử dụng kiến thức:

+) Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

+) Trong một đường tròn, số đo góc nội tiếp bằng nửa số đo của góc ở tâm chắn cùng chắn một cung.

Lời giải chi tiết

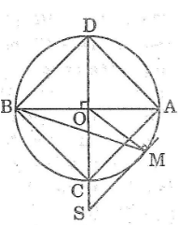
Xét đường tròn \((O)\) có \(SM \bot OM\) (tính chất tiếp tuyến)

\( \Rightarrow \Delta OMS\) vuông tại \(M\)

Nên \(\widehat {MSO} + \widehat {MOS} = {90^o}\)

Lại có: \(AB \bot CD\) \((gt)\)

\( \Rightarrow \widehat {MOS} + \widehat {MOA} = {90^o}\)

Suy ra: \(\widehat {MSO} = \widehat {MOA}\) hay \(\widehat {MSD} = \widehat {MOA}\) \((1)\)

Mà \(\widehat {MOA} = 2\widehat {MBA}\)  (góc ở tâm và góc nội tiếp cùng chắn cung \(\overparen{AM}\))  \((2)\)

Từ \((1)\) và \((2)\) suy ra: \(\widehat {MSD} = 2\widehat {MBA}\)

-- Mod Toán 9 HỌC247