Giải bài 19 tr 68 sách GK Toán 8 Tập 2
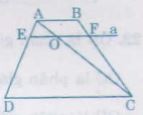
Cho hình thang \(ABCD\) (\(AB // CD\)).
Đường thẳng \(a\) song song với \(DC\), cắt các cạnh \(AD\) và \(BC\) theo thứ tự là \(E\) và \(F.\)
Chứng minh rằng:
a) \(\dfrac{AE}{ED} = \dfrac{BF}{FC}\);
b) \(\dfrac{AE}{AD} = \dfrac{BF}{BC}\)
c) \(\dfrac{DE}{DA} = \dfrac{CF}{CB}\).
Hướng dẫn giải chi tiết
a) Nối \(AC\) cắt \(EF\) tại \(O\)
\(∆ADC\) có \(EO // DC\) (giả thiết) \( \Rightarrow \dfrac{AE}{ED} = \dfrac{AO}{OC}\) (1) (theo định lí Talet)
\(∆ABC\) có \(OF // AB\) (giả thiết) \( \Rightarrow \dfrac{AO}{OC} = \dfrac{BF}{FC}\) (2) (theo định lí Talet)
Từ (1) và (2) \(\Rightarrow \dfrac{AE}{ED} = \dfrac{BF}{FC}\)
b) Theo câu a) ta có:
\(\eqalign{
& {{AE} \over {ED}} = {{BF} \over {FC}} \Rightarrow {{FC} \over {BF}} = {{ED} \over {AE}} \cr
& \Rightarrow {{FC} \over {BF}} + 1 = {{ED} \over {AE}} + 1 \cr
& \Rightarrow {{FC + BF} \over {BF}} = {{ED + AE} \over {AE}} \cr
& \Rightarrow {{BC} \over {BF}} = {{AD} \over {AE}} \cr
& \Rightarrow {{AE} \over {AD}} = {{BF} \over {BC}} \cr} \)
c) Theo câu b) ta có:
\(\eqalign{
& {{AE} \over {ED}} = {{BF} \over {FC}} \cr
& \Rightarrow {{AE} \over {ED}} + 1 = {{BF} \over {FC}} + 1 \cr
& \Rightarrow {{AE + ED} \over {ED}} = {{BF + FC} \over {FC}} \cr
& \Rightarrow {{AD} \over {ED}} = {{BC} \over {FC}} \cr
& \Rightarrow {{FC} \over {BC}} = {{ED} \over {AD}}\,\,\,hay\,\,{{DE} \over {DA}} = {{CF} \over {CB}} \cr} \)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 17 trang 68 SGK Toán 8 Tập 2
Bài tập 18 trang 68 SGK Toán 8 Tập 2
Bài tập 20 trang 68 SGK Toán 8 Tập 2
Bài tập 21 trang 68 SGK Toán 8 Tập 2
Bài tập 22 trang 68 SGK Toán 8 Tập 2
Bài tập 17 trang 87 SBT Toán 8 Tập 2
Bài tập 18 trang 87 SBT Toán 8 Tập 2
Bài tập 19 trang 87 SBT Toán 8 Tập 2
Bài tập 20 trang 87 SBT Toán 8 Tập 2
Bài tập 21 trang 88 SBT Toán 8 Tập 2
Bài tập 22 trang 88 SBT Toán 8 Tập 2
Bài tập 23 trang 88 SBT Toán 8 Tập 2
Bài tập 24 trang 88 SBT Toán 8 Tập 2
-


Cho tam giác ABC vuông tại A đường phân giác AD. Tính độ dài AB, AC biết BC = 15cm DC = 20cm.
bởi Minh Tiến
 04/04/2020
Giải hộ mìnhTheo dõi (0) 17 Trả lời
04/04/2020
Giải hộ mìnhTheo dõi (0) 17 Trả lời -

 Cho tam giác ABC có AB = 14 , AC = 21, AD LÀ PHÂN GIÁC GÓC A. AD =8 tính BCTheo dõi (0) 4 Trả lời
Cho tam giác ABC có AB = 14 , AC = 21, AD LÀ PHÂN GIÁC GÓC A. AD =8 tính BCTheo dõi (0) 4 Trả lời -


Cho tam giác ABC vuông tại A, đường phân giác BD. Biết AD=3cm; DC=5cm. Tính độ dài các cạnh AB, BC?
bởi Hà Vi Trang
 26/03/2020
26/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A, AB=12cm, AC=16cm. Đường phân giác góc A cắt BC ở D. Tính BC, BD, CD.
bởi An Truong
 25/03/2020
25/03/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho tam giác ABC có AD là tia phân giác. Biết AB=15cm, DC=21cm, BD=9cm. Tính AC.
bởi An Truong
 25/03/2020
25/03/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời