Giải bài 19 trang 87 SBT Toán 8 Tập 2
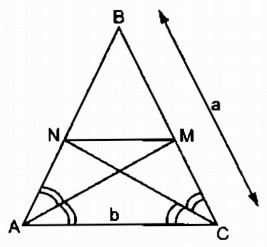
Tam giác cân \(BAC\) có \(BA = BC = a, AC = b.\) Đường phân giác góc \(A\) cắt \(BC\) tại \(M\), đường phân giác góc \(C\) cắt \(BA\) tại \(N\) (h16).
a) Chứng minh rằng: \(MN // AC.\)
b) Tính \(MN\) theo \(a, b\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Tính chất đường phân giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy.
- Định lí đảo của định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
- Hệ quả của định lí Ta-lét: Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
Lời giải chi tiết
a) Xét \(\Delta BAC\) có \(AM\) là đường phân giác của \(\widehat {BAC}\)
\(\Rightarrow \displaystyle{{MC} \over {MB}} = {{AC} \over {AB}}\) (tính chất đường phân giác ) (1)
\(CN\) là đường phân giác của \(\widehat {BCA}\)
\(\Rightarrow \displaystyle{{NA} \over {NB}} = {{AC} \over {BC}}\) (tính chất đường phân giác ) (2)
Lại có: \(AB = CB = a\) (gt) (3)
Từ (1), (2) và (3) suy ra: \(\displaystyle {{MC} \over {MB}} = {{NA} \over {NB}}\)
Xét \(\Delta BAC\) có \(\displaystyle {{MC} \over {MB}} = {{NA} \over {NB}}\) nên theo định lí đảo của định lí Ta-lét ta có \(MN // AC\).
b) Ta có: \(\displaystyle {{MC} \over {MB}} = {{AC} \over {AB}}\) (chứng minh trên )
\( \Rightarrow \dfrac{{MC}}{{MB}} + 1 = \dfrac{{AC}}{{AB}} + 1\)
\(\Rightarrow \displaystyle {{MC + MB} \over {MB}} = {{AC + AB} \over {AB}} \)
\(\Rightarrow \displaystyle {{CB} \over {MB}} = {{AC + AB} \over {AB}}\)
\(\Rightarrow \displaystyle{a \over {MB}} = {{b + a} \over a}\)
\(\Rightarrow \displaystyle MB = {{{a^2}} \over {a + b}}\)
Xét \(\Delta BAC\) có \(MN // AC\) (chứng minh trên)
Theo hệ quả của định lí Ta-lét ta có: \(\displaystyle {{MN} \over {AC}} = {{MB} \over {BC}}\)
\( \Rightarrow MN = \dfrac{{AC.MB}}{{BC}} = \dfrac{{b.\dfrac{{{a^2}}}{{a + b}}}}{a} \)\(\,= \dfrac{{ab}}{{a + b}}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Chứng minh DB/DC.EC/EA.FA/FB=1
bởi Tay Thu
 31/05/2019
31/05/2019
Tam giác ABC có các đường phân giác AD,BE,CF.
Cmr:DB/DC.EC/EA.FA/FB=1
Theo dõi (0) 1 Trả lời -


Cho tam giác cân abc(ab=ac)có đường phân giác BD và cho biết rằng:AB=AC=10cm,BC=10cm
a) Tính độ dài của AB,CD
b)Đường vuông góc với BD tại B cắt đường thẳng AC kéo dài tại E.
Tính độ dài của đoạn thẳng CE
Theo dõi (0) 1 Trả lời -


Tính độ dài BD biết AD=DE=EC
bởi Lê Tấn Vũ
 31/07/2019
31/07/2019
cho tam giác ABC vuông tại A ,AB =1cm ,AC=3cm.Trên cạnh AC lấy dm D,E sao cho AD=DE=EC
â) Tính độ dài BD
b) CM:tam giác BDE đồng dạng vs tam giác CDB
c) Tinh DEB+DCB
Theo dõi (0) 1 Trả lời -


1. Cho \(\Delta\)ABC, phân giác BD. Qua D vẽ đường thẳng song song vs BC cắt AB ở I. Biết DI=6; BC=10. Tính AB
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh ID là phân giác cua AIC
bởi Lê Tấn Vũ
 31/05/2019
31/05/2019
Cho hình bình hành ABCD. E thuộc AB, F thuộc BC sao cho AF=CE. I là giao điểm của AF và CE. Chứng minh ID là phân giác cua AIC
HELP ME!!!!
Theo dõi (0) 1 Trả lời


