Trong bài học này chúng ta sẽ làm quen với Định lí Thalès trong tam giác trong tam giác. Thông qua đó, các em sẽ nhận biết được định lí Thalès đồng thời biết cách áp dụng định lí Thalès vào các bài toán tính độ dài cạnh trong tam giác và các bài toán thực tiễn. Đây là một bài toán căn bản giúp các em học tốt các phần tiếp theo. Chúc các em học thật tốt!
Tóm tắt lý thuyết
1.1.Đoạn thẳng tỉ lệ
Tỉ số hai đoạn thẳng
|
- Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo. - Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là: \(\frac{{AB}}{{CD}}\). |
Chú ý:
- Để tính tỉ số của hai đoạn thẳng, ta phải đưa chúng về cùng một đơn vị đo.
- Tỉ số của hai đoạn thẳng đó không phụ thuộc vào đơn vị đo độ dài đoạn thẳng.
Đoạn thẳng tỉ lệ
|
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng EF và MN nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{EF}}{{MN}}\) hay \(\frac{{AB}}{{EF}} = \frac{{CD}}{{MN}}\). |
1.2. Định lí Thalès trong tam giác
Định lí Thalès
| Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương đương tỉ lệ. |
| GT | \(\Delta ABC,B'C'//BC(B' \in AB,C' \in AC)\) |
| KL | \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}};\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}};\frac{{B'B}}{{AB}} = \frac{{C'C}}{{AC}}\) |
Hệ quả của định lí Thalès
|
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh thứ ba thì tạo ra một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho. |
| GT | \(\Delta ABC,B'C'//BC(B' \in AB,C' \in AC)\) |
| KL | \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\) |
Định lí Thalès đảo
|
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. |
| GT |
\(\Delta ABC,B' \in AB,C' \in AC\) \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}}\) |
| KL | \(B'C'//BC\) |
Bài tập minh họa
Bài 1. Cho tam giác ABC. Trên cạnh BC lấy điểm D sao cho BC = 2BD. Trên đoạn AD lấy điểm O sao cho . Gọi I là giao điểm của CO và AB. Tính tỉ số ?
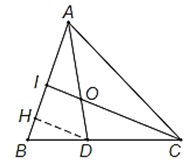
Hướng dẫn giải
Kẻ thêm DH // CI (H thuộc AB) thì DH // IO.
Áp dụng định lí Thalès vào ∆ADH có DH // IO, ta có:
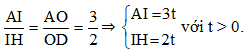
Ta có: BD + DC = BC, suy ra DC = BC – BD = 2BD – BD = BD nên BC = 2DC.
Áp dụng định lí Thalès vào ∆BIC có DH // IC, ta có:
⇒ BI = 2IH = 2 . 2t = 4t
Vậy .
Bài 2. Tìm độ dài x cho hình vẽ dưới đây biết MN // BC?
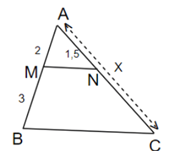
Hướng dẫn giải
Ta có: AB = AM + MB = 2 + 3 = 5.
Áp dụng định lí Thalès trong tam giác ABC có MN // BC
Ta có: ⇒ ⇒ x = = 3,75.
Vậy x = 3,75.
3. Luyện tập Bài 1 Chương 7 Toán 8 Chân trời sáng tạo
Qua bài học này, các em sẽ có thể hoàn thành một số mục tiêu mà bài đưa ra như sau:
- Định lí Thalès trong tam giác (thuận và đảo).
- Tính độ dài đoạn thẳng bằng cách sử dụng Định lí Thalès.
- Giải quyết một số vấn đề thực tiễn gắn với việc vận dụng định lí Thalès.
3.1 Trắc nghiệm Bài 1 Chương 7 Toán 8 Chân trời sáng tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 8 Chân trời sáng tạo Chương 7 Bài 1 cực hay có đáp án và lời giải chi tiết.
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK Bài 1 Chương 7 Toán 8 Chân trời sáng tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 8 Chân trời sáng tạo Chương 7 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Khởi động trang 44 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Khám phá 1 trang 44 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 1 trang 44 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Khám phá 2 trang 45 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 2 trang 45 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 1 trang 45 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Khám phá 3 trang 45 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 3 trang 46 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Khám phá 4 trang 47 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 4 trang 48 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 2 trang 48 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Khám phá 5 trang 48 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 5 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 3 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 1 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 2 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 3 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 4 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 5 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 6 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 7 trang 51 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 8 trang 51 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 9 trang 51 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
4. Hỏi đáp Bài 1 Chương 7 Toán 8 Chân trời sáng tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 8 HỌC247


.PNG)
.PNG)
.PNG)
.PNG)


