Khám phá 5 trang 48 SGK Toán 8 Chân trời sáng tạo Tập 2
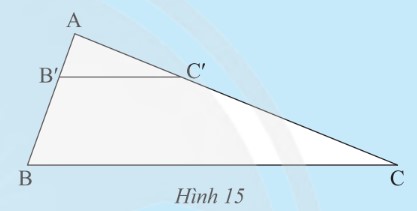
Cho tam giác \(ABC\) có \(AB = 6~cm, AC = 15~cm\). Trên \(AB, AC\) lần lượt lấy \(B', C'\) sao cho \(AB' = 2~cm, AC' = 5~cm\).
a) Tính các tỉ số \(\frac{AB'}{AB}\) và \(\frac{AC'}{AC}\)?
b) Qua B' vẽ đường thẳng song song với BC cắt AC tại E. Tính AE?
c) So sánh AE và AC'?
d) Hãy nhận xét về vị trí của E và C', vị trí của hai đường thẳng B'C' và B'E?
Hướng dẫn giải chi tiết Khám phá 5
a) Ta có:
\(\frac{AB'}{AB}=\frac{2}{6}=\frac{1}{3}\)
\(\frac{AC'}{AC}=\frac{5}{15}=\frac{1}{3}\)
b) Xét tam giác BC có: B'E // BC , theo định lí Thales ta có:
\(\frac{AB'}{AB}=\frac{AE}{AC}\)
\(\Leftrightarrow \frac{1}{3}=\frac{AE}{15}\)
\(\Leftrightarrow AE = 5~cm\)
c) Ta có: \(AE = AC' = 5~cm\).
d) Vì E và C' cùng thuộc AC và \(AE = AC'\) suy ra E và C' trùng nhau, B'C' và B'E trùng nhau.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Thực hành 4 trang 48 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 2 trang 48 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 5 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Vận dụng 3 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 1 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 2 trang 49 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 3 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 4 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 5 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 6 trang 50 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 7 trang 51 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 8 trang 51 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 9 trang 51 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


