HЖ°б»ӣng dбә«n GiбәЈi bГ i tбәӯp ToГЎn 7 Kбәҝt nб»‘i tri thб»©c BГ i tбәӯp cuб»‘i chЖ°ЖЎng 9 giГәp cГЎc em hб»Қc sinh nбәҜm vб»Ҝng phЖ°ЖЎng phГЎp giбәЈi bГ i tбәӯp vГ Гҙn luyб»Үn tб»‘t kiбәҝn thб»©c.
-
GiбәЈi bГ i 9.36 trang 84 SGK ToГЎn 7 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 2 - KNTT
Cho tam giГЎc ABC \(\widehat{BAC}\) lГ gГіc tГ№. LбәҘy Д‘iб»ғm D nбәұm giб»Ҝa A vГ B, lбәҘy Д‘iб»ғm E nбәұm giб»Ҝa A vГ C (H.9.51). Chб»©ng minh DE < BC.
-
GiбәЈi bГ i 9.37 trang 84 SGK ToГЎn 7 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 2 - KNTT
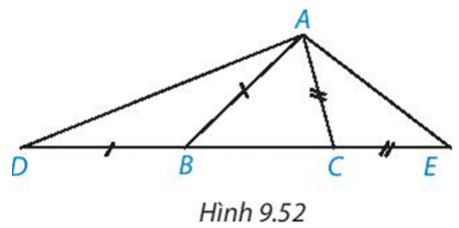
Cho tam giГЎc ABC ( AB> AC). TrГӘn Д‘Ж°б»қng thбәіng chб»©a cбәЎnh BC, lбәҘy Д‘iб»ғm D vГ Д‘iб»ғm E sao cho B nбәұm giб»Ҝa B D vГ C, C nбәұm giб»Ҝa B vГ E, BD = BA, CE= CA ( H.9.52)
a) So sГЎnh \(\widehat{ADE}\) vГ \(\widehat{AED}\)
b) So sГЎnh cГЎc Д‘oбәЎn thбәіng AD vГ AE
-
GiбәЈi bГ i 9.38 trang 84 SGK ToГЎn 7 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 2 - KNTT
Gб»Қi AI vГ AM lбә§n lЖ°б»Јt lГ Д‘Ж°б»қng cao vГ Д‘Ж°б»қng trung tuyбәҝn xuбәҘt phГЎt tб»« Д‘б»үnh A của tam giГЎc ABC. Chб»©ng minh rбәұng
a) AI < \(\frac{1}{2}\) (AB + AC)
b) AM < \(\frac{1}{2}\) (AB + AC)
-
GiбәЈi bГ i 9.39 trang 84 SGK ToГЎn 7 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 2 - KNTT
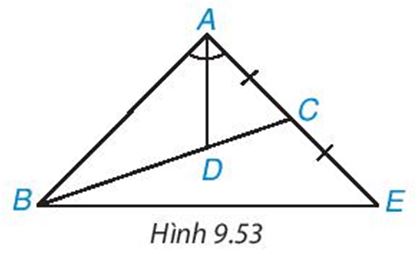
Cho tam giГЎc ABC cГі Д‘Ж°б»қng phГўn giГЎc AD, D nбәұm trГӘn BC sao cho BD= 2 DC. TrГӘn Д‘Ж°б»қng thбәіng AC, lбәҘy Д‘iб»ғm E sao cho C lГ trung Д‘iб»ғm của AE (H.9.53). Chб»©ng minh rбәұng tam giГЎc ABE cГўn tбәЎi A
Gб»Јi ГҪ D lГ trб»Қng tГўm của tam gГӯac ABE, tam giГЎc nГ y cГі Д‘Ж°б»қng phГўn giГЎc AD Д‘б»“ng thб»қi lГ trung tuyбәҝn.
- VIDEOYOMEDIA
-
GiбәЈi CГўu hб»Ҹi 1 trang 59 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Tìm phương án Sai trong câu sau: Trong tam giác
A.Д‘б»‘i diб»Үn vб»ӣi gГіc lб»ӣn nhбәҘt lГ cбәЎnh lб»ӣn nhбәҘt
B.Д‘б»‘i diб»Үn vб»ӣi cбәЎnh bГ© nhбәҘt lГ gГіc nhб»Қn
C.Д‘б»‘i diб»Үn vб»ӣi cбәЎnh lб»ӣn nhбәҘt lГ gГіc tГ№
D.Д‘б»‘i diб»Үn vб»ӣi gГіc tГ№ (nбәҝu cГі) lГ cбәЎnh lб»ӣn nhбәҘt.
-
GiбәЈi CГўu hб»Ҹi 2 trang 59 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Bб»ҷ ba sб»‘ nГ o sau Д‘Гўy khГҙng lГ Д‘б»ҷ dГ i ba cбәЎnh của mб»ҷt tam giГЎc?
A.7, 5, 7
B.7, 7, 7
C.3, 5, 4
D.4, 7, 3
-
GiбәЈi CГўu hб»Ҹi 3 trang 59 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Tam giГЎc cГўn cГі Д‘б»ҷ dГ i cбәЎnh bГӘn b, Д‘б»ҷ dГ i cбәЎnh Д‘ГЎy d thГ¬ ta phбәЈi cГі:
A.d > b
B.d = 2b
C.d < b/2
D. d < 2b
-
GiбәЈi CГўu hб»Ҹi 4 trang 59 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Vб»ӣi mб»Қi tam giГЎc ta Д‘б»Ғu cГі:
A.mб»—i cбәЎnh lб»ӣn hЖЎn nб»ӯa chu vi
B.mб»—i cбәЎnh lб»ӣn hЖЎn hoбә·c bбәұng nб»ӯa chu vi
C.mб»—i cбәЎnh nhб»Ҹ hЖЎn nб»ӯa chu vi
D.cбәЈ ba trЖ°б»қng hб»Јp trГӘn Д‘б»Ғu cГі thб»ғ xбәЈy ra.
-
GiбәЈi CГўu hб»Ҹi 5 trang 59 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
XГ©t hai Д‘Ж°б»қng trung tuyбәҝn BM, CN của tam giГЎc ABC cГі BC = 4cm. Trong cГЎc sб»‘ sau, sб»‘ nГ o cГі thб»ғ lГ tб»•ng Д‘б»ҷ dГ i BM + CN?
A.5 cm
B.5,5 cm
C.6 cm
D.6,5 cm
-
GiбәЈi CГўu hб»Ҹi 6 trang 59 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Tam giГЎc ABC cГі sб»‘ Д‘o ba gГіc thoбәЈ mГЈn: \(\widehat A = \widehat B + \widehat C\). Hai tia phГўn giГЎc của gГіc A vГ gГіc B cбәҜt nhau tбәЎi Д‘iб»ғm I. Khi Д‘Гі gГіc BIC cГі sб»‘ Д‘o lГ :
A.\({120^0}\)
B. \({125^0}\)
C. \({130^0}\)
D. \({135^0}\)
-
GiбәЈi bГ i 9.23 trang 60 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Cho D lГ mб»ҷt Д‘iб»ғm bГӘn trong tam giГЎc ABC. Chб»©ng minh:
a)\(\widehat {BDC} > \widehat {BAC}\)
b) BD + DC < AB + AC
-
GiбәЈi bГ i 9.24 trang 60 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Cho M lГ mб»ҷt Д‘iб»ғm tuб»і ГҪ bГӘn trong tam giГЎc Д‘б»Ғu ABC. LбәҘy Д‘iб»ғm N nбәұm khГЎc phГӯa vб»ӣi M Д‘б»‘i vб»ӣi Д‘Ж°б»қng thбәіng AC sao cho \(\widehat {CAN} = \widehat {BAM}\) vГ AN = AM.
Chб»©ng minh:
a) Tam giГЎc AMN lГ tam giГЎc Д‘б»Ғu
b) \(\Delta MAB = \Delta NAC\)
c) MN = MA, NC = MB
-
GiбәЈi bГ i 9.25 trang 60 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
XГ©t tam giГЎc ABC vuГҙng tбәЎi A; Д‘Ж°б»қng phГўn giГЎc gГіc B cбәҜt cбәЎnh AC tбәЎi E; Д‘Ж°б»қng thбәіng qua E vuГҙng gГіc vб»ӣi BC cбәҜt Д‘Ж°б»қng thбәіng AB tбәЎi K. Chб»©ng minh:
a)AE < EC
b) BK = BC.
-
GiбәЈi bГ i 9.26 trang 60 SBT ToГЎn 7 Kбәҝt nб»‘i tri thб»©c tбәӯp 2 - KNTT
Cho C lГ trung Д‘iб»ғm của Д‘oбәЎn thбәіng AB. Gб»Қi Ax, By lГ hai Д‘Ж°б»қng thбәіng vuГҙng gГіc vб»ӣi AB tбәЎi A vГ tбәЎi B. Mб»ҷt Д‘Ж°б»қng thбәіng qua C cбәҜt Ax tбәЎi M, cбәҜt By tбәЎi P. Дҗiб»ғm N nбәұm trГӘn tia Д‘б»‘i của tia BP sao cho gГіc MCN lГ gГіc vuГҙng. Gб»Қi H lГ hГ¬nh chiбәҝu của C trГӘn MN.
Chб»©ng minh:
a)AM + BN = MN;
b) CM lГ Д‘Ж°б»қng trung trб»ұc của AH, CN lГ Д‘Ж°б»қng trung trб»ұc của BH;
c) GГіc AHB lГ gГіc vuГҙng.