Giải Câu hỏi 6 trang 59 SBT Toán 7 Kết nối tri thức tập 2
Tam giác ABC có số đo ba góc thoả mãn: \(\widehat A = \widehat B + \widehat C\). Hai tia phân giác của góc A và góc B cắt nhau tại điểm I. Khi đó góc BIC có số đo là:
A.\({120^0}\)
B. \({125^0}\)
C. \({130^0}\)
D. \({135^0}\)
Hướng dẫn giải chi tiết
Phương pháp giải:
Áp dụng định lí về tổng ba góc trong tam giác; tính chaasrt tia phân giác của một góc.
Lời giải chi tiết:
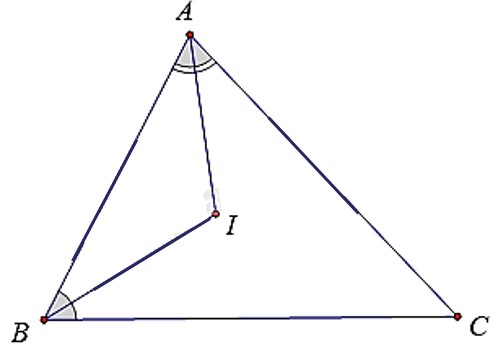
Ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)(Tổng ba góc trong tam giác)
Mà \(\widehat A = \widehat B + \widehat C\)
\(\begin{array}{l} \Rightarrow \left( {\widehat B + \widehat C} \right) + \widehat B + \widehat C = {180^0}\\ \Rightarrow 2\left( {\widehat B + \widehat C} \right) = {180^0}\\ \Rightarrow \widehat B + \widehat C = {180^0}:2 = {90^0}\\ \Rightarrow \widehat A = \widehat B + \widehat C = {90^0}\end{array}\)
Xét tam giác BIC có:
\(\widehat {BIC} = {180^0} - \left( {\widehat {\dfrac{B}{2}} + \dfrac{{\widehat C}}{2}} \right) = {180^0} - \dfrac{{{{90}^0}}}{2} = {180^0} - {45^0} = {135^0}\).
Chọn D.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải Câu hỏi 4 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải Câu hỏi 5 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.23 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.24 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.25 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.26 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


