Giải bài 9.38 trang 84 SGK Toán 7 Kết nối tri thức tập 2
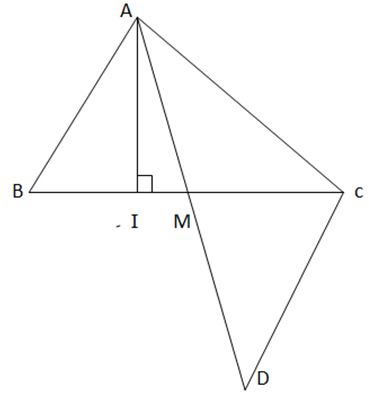
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng
a) AI < \(\frac{1}{2}\) (AB + AC)
b) AM < \(\frac{1}{2}\) (AB + AC)
Hướng dẫn giải chi tiết Giải bài 9.38
Phương pháp giải
a) AI là đường cao từ A xuống đoạn thẳng BC
=> AI < AB và AI < AC
Cộng 2 vế với nhau ta có => AI <\(\frac{1}{2}\) (AB + AC)
b) Lấy D sao cho M là trung điểm của AD
Xét ∆ ABM và ∆ DCM, chứng minh ∆ ABM = ∆ DCM
Lời giải chi tiết
a) AI là đường cao từ A xuống đoạn thẳng BC=> AI là khoảng cách từ A đến BC => AI ngắn nhất
=> AI < AB và AI < AC
Cộng 2 vế với nhau ta có : 2 AI < AB + AC
=> AI <\(\frac{1}{2}\) (AB + AC)
b) Lấy D sao cho M là trung điểm của AD
Xét ∆ ABM và ∆ DCM có
AM = DM ( M là trung điểm củaAD)
BM=CM ( M là trung điểm của BC)
\(\widehat{AMB}\) = \(\widehat{CMD}\) (2 góc đối đỉnh)
=> ∆ ABM = ∆ DCM
=>AB = CD
Xét ∆ ADC ta có: AD < AC + CD
=> 2AM < AC + AB
=> AM < \(\frac{1}{2}\) (AB + AC)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 9.36 trang 84 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.37 trang 84 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.39 trang 84 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải Câu hỏi 1 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải Câu hỏi 2 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải Câu hỏi 3 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải Câu hỏi 4 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải Câu hỏi 5 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải Câu hỏi 6 trang 59 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.23 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.24 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.25 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.26 trang 60 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.