Giải bài 2 tr 137 sách BT Toán lớp 7 Tập 1
Cho tam giác ABC có \(\widehat A = 60^\circ ,\widehat C = 50^\circ \). Tia phân giác của góc B cắt AC ở D. Tính \(\widehat {ADB},\widehat {CDB}\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Định lí: Tổng ba góc của một tam giác bằng \({180^0}\).
Lời giải chi tiết
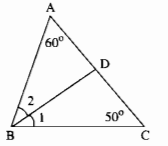
Trong ∆ABC ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng 3 góc trong tam giác)
\(\eqalign{
& \Rightarrow \widehat B = 180^\circ - \left( {\widehat A + \widehat C} \right) \cr
& \Rightarrow x = 180^\circ - \left( {60^\circ + 50^\circ } \right) = 70^\circ \cr} \)
\(\widehat {{B_1}} = \widehat {{B_2}} = {1 \over 2}\widehat B\) (Vì BD là tia phân giác)
\( \Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = 70^\circ :2 = 35^\circ \)
Trong ∆BDC ta có \(\widehat {A{\rm{D}}B}\) là góc ngoài tại đỉnh D.
\( \Rightarrow \widehat {A{\rm{D}}B} = \widehat {{B_1}} + \widehat C\) (tính chất góc ngoài tam giác)
\( \Rightarrow \widehat {A{\rm{D}}B} = 35^\circ + 50^\circ = 85^\circ \)
\(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {B{\rm{D}}C} = 180^\circ - \widehat {A{\rm{D}}B} = 180^\circ - 85^\circ = 95^\circ \)
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Bài tập 9 trang 109 SGK Toán 7 Tập 1
Bài tập 1 trang 137 SBT Toán 7 Tập 1
Bài tập 3 trang 137 SBT Toán 7 Tập 1
Bài tập 4 trang 137 SBT Toán 7 Tập 1
Bài tập 5 trang 137 SBT Toán 7 Tập 1
Bài tập 6 trang 137 SBT Toán 7 Tập 1
Bài tập 7 trang 137 SBT Toán 7 Tập 1
Bài tập 8 trang 138 SBT Toán 7 Tập 1
Bài tập 9 trang 138 SBT Toán 7 Tập 1
Bài tập 10 trang 138 SBT Toán 7 Tập 1
Bài tập 11 trang 138 SBT Toán 7 Tập 1
Bài tập 12 trang 138 SBT Toán 7 Tập 1
Bài tập 13 trang 138 SBT Toán 7 Tập 1
Bài tập 14 trang 138 SBT Toán 7 Tập 1
Bài tập 15 trang 138 SBT Toán 7 Tập 1
Bài tập 16 trang 139 SBT Toán 7 Tập 1
-


Tính số đo các góc của tam giác MNP biết M=3x, N=2x, P=4x
bởi can chu
 22/02/2019
22/02/2019
Tính số đo các góc của tam giác MNP biết,
góc M= 3x, góc N= 2x, góc P= 4x.
Giúp mik vs mik cần gấp lắm thanks nhiều nha
Theo dõi (0) 1 Trả lời -


Tính góc C của tam giác ABC có A=78 độ, B=64 độ
bởi Lê Minh
 22/02/2019
22/02/2019
Cho ABC
Biet\(\widehat{A}\) = 78 ,\(\widehat{B}\) =64 Tinh \(\widehat{C}\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có góc A bằng 80độ, góc B bằng 60độ
a, so sánh các cạnh của tam giác ABC
b, trên BC lấy điểm M sao cho BM=BA .Tia phân giác góc B cắt AC tại D .CM: ∆BAD=∆BM.
c, Tia MD cắt tại BA tại H, CM ∆DHM cân
d, CM BD>AM và tính số đo góc DHC
Các bn giúp mik nhé mai mik nộp r
Theo dõi (0) 1 Trả lời -


Bài 4: Cho tam giác ABC, điểm M nằm trong tam giác đó. Tia BM cắt AC ở K
a) So sánh góc AMK và góc ABK
b) So sánh góc AMC và góc ABC
Theo dõi (0) 1 Trả lời -
ADMICRO


Bài 1: Cho tam giác ABC có A = 90*, B = 60*. Tia phân giác của A cắt BC ở D. Kẻ AH vuông góc BC ( H thuộc BC )
a) Tính C
b) Tính ADH
c) Tính HAD
d) So sánh HAC và ABC
Theo dõi (0) 1 Trả lời -


Tính tổng ba góc ngoài tại ba đỉnh của một tam giác
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại a ,trên nửa mặt phẳng bờ BC (không chứa A ),kẻ tia Bx sao cho xBC=BCA
a)Chứng tỏ AC//Bx
b)Chứng minh AB vuông góc với Bx
c )Trên tia Bx lấy điểm D sao cho góc ACD =120 dộ.Tính góc CDB,góc CDx?
help me

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


cho tam giác ABC có góc B lớn hơn góc C , kẻ AH vuông góc vs BC (H thuộc BC), Tia pg AD của góc BAC(D thuộc BC). tính góc DAH theo góc B và C của tam giác ABC
Theo dõi (0) 1 Trả lời -


Cho \(\Delta\)ABC có 10 lần góc A = 2 lần góc B = \(\dfrac{5}{3}\)lần góc C . Tính số đo mỗi góc của \(\Delta\)ABC .
Theo dõi (0) 1 Trả lời -


C/m : \(\widehat{CAx}=\widehat{B}+\widehat{C}\)Theo dõi (0) 1 Trả lời -


1. Tính các góc của tam giác ABC, biết rằng góc A trừ góc B bằng 18 độ và góc B trừ góc C bằng 18 độ.
Theo dõi (0) 1 Trả lời



