Giải bài 17 tr 139 sách BT Toán lớp 7 Tập 1
Chứng minh rằng nếu một đường thẳng cắt hai đường thẳng song song thì hai tia phân giác của cặp góc trong cùng phía vuông góc với nhau.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Định lí: Tổng ba góc của một tam giác bằng \({180^0}\).
- Một đường thẳng cắt hai đường thẳng song song tạo ra cặp góc trong cùng phía bù nhau.
Lời giải chi tiết
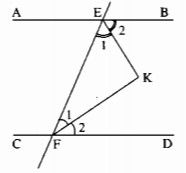
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F
Ta có: \(\widehat {BEF} + \widehat {EFD} = 180^\circ \) (hai góc trong cùng phía)
\(\eqalign{
& \widehat {{E_1}} = {1 \over 2}\widehat {{\rm{BEF}}}\left( {gt} \right) \cr
& \widehat {{F_1}} = {1 \over 2}\widehat {EFD}\left( {gt} \right) \cr} \)
\( \Rightarrow \widehat {{E_1}} + \widehat {{F_1}} = {1 \over 2}\left( {\widehat {{\rm{BEF}}} + \widehat {EFD}} \right) = 90^\circ \)
Trong ∆EKF, ta có:
\(\widehat {EKF} = 180^\circ - \left( {\widehat {{E_1} + \widehat {{F_1}}}} \right) = 180^\circ - 90^\circ = 90^\circ \)
Vậy \(EK \bot FK\).
-- Mod Toán 7 HỌC247
Bài tập SGK khác
-
Góc G và góc H là bao nhiêu độ biết góc G và góc H là 2 góc phụ nhau?
bởi Lê Nguyễn Hạ Anh
01/02/2020
Biết góc G và góc H là 2 góc phụ nhau . Nếu góc G = 3x+6 và góc H = 2x-11. Hỏi gốc G và góc H là bao nhiêu độ
Theo dõi (0) 1 Trả lời -
Tính số đo góc A biết tia phân giác các góc B, C cắt AB, AC lần lượt tại M va N
bởi Sam sung
01/02/2020
cho tam giac ABC. Tia phân giác các góc B, C cắt AB, AC lần lượt tại M va N. Giả sử BN+CM=BC. Tính số đo góc A
Theo dõi (0) 1 Trả lời -
Tính góc AED biết tam giác ABC có góc A=64, B=80
bởi Mai Rừng
01/02/2020
Cho tam giác ABC có góc A=64, B=80. Phân giác góc A cắt BC tại D. Kẻ Dx song song với AB, Dx cắt AC tại E. Tính góc AED
Theo dõi (0) 1 Trả lời -
cho góc BAx có số đo bằng 60o. Từ A kẻ At vuống góc với Ax, từ B kẻ đường thẳng d vuông góc với AB cắt Ax, At lần lượt tại C, D tỉ số giữa số đo góc ADC và góc ACB bằng
Theo dõi (0) 1 Trả lời -
ADMICRO
ai giải hộ em bài này vs
Theo dõi (0) 2 Trả lời -
Cho tam giác ABC có góc B > C, đt chứa tia phân giác của góc ngoài đỉnh A cắt đt BC ở E
bởi thu phương
21/03/2018
Hi mấy bạn, có bạn nào cứu mình bài này không
Cho tam giác ABC có \(\widehat B > \widehat C\). Đường thẳng chứa tia phân giác của góc ngoài đỉnh A cắt đường thẳng BC ở E.
a. Chứng minh \(\widehat {{\rm{AEB}}} = \frac{1}{2}(\widehat B - \widehat C)\)
b. Từ B dựng đường thẳng song song với AE, cắt cạnh AC ở k. Chứng minh tam giác ABK có hai góc bằng nhau.
Theo dõi (0) 2 Trả lời -
giúp e vs ạ
Chứng minh rằng tổng ba góc ngoài của một tam giác bằng 4 vuông.
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC có góc B, C = 50, gọi Am là tia phân giác của góc ngoài ở điểm A
bởi ngọc trang
22/03/2018
M.n ơi giúp mình bài này với
Cho tam giác ABC có \(\widehat B = \widehat C = {50^0} \). Gọi Am là tia phân giác của góc ngoài ở điểm A. Hãy chứng minh tỏ rằng Am // BC.
Theo dõi (0) 1 Trả lời -
Tìm số đo các góc của tam giác ABC
bởi bich thu
21/03/2018
Giúp tại hạ với !!!
Tìm số đo các góc của tam giác ABC biết rằng: \(21\widehat C = 14\widehat B = 6\widehat C\)
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC về tia phân giác AD của góc A, tính các góc của tam giác ABC
bởi minh vương
21/03/2018
mọi người ai biết chỉ mình với nhé
Cho tam giác ABC về tia phân giác AD của góc A, biết \(\widehat {ADB} = {80^0}\) và \(\widehat B = \frac{3}{2}\widehat C\). Tính các góc của tam giác ABC.
Theo dõi (0) 1 Trả lời -
Cho điểm O trong tam giác ABC, cmr BOC > A
bởi minh dương
21/03/2018
ai chứng minh hộ mình câu này vs
Cho điểm O trong tam giác ABC. Chứng minh rằng \(\widehat {BOC}{\rm{ }} > {\rm{ }}\widehat A\).
Theo dõi (0) 2 Trả lời
