Phần hướng dẫn giải bài tập SGK bài 1 chương IV Giới hạn của dãy số sẽ giúp các em nắm được phương pháp giải các bài tập từ SGK Đại số và Giải tích 11 Cơ bản và Nâng cao.
-
Bài tập 1 trang 121 SGK Đại số & Giải tích 11
Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24 000 năm thì một nửa số chất phóng xạ này bị phân rã thành chất khác không độc hại đối với sức khỏe của con người (T được gọi là chu kì bán rã). Gọi un là khối lượng chất phóng xạ còn sót lại sau chu kì thứ n.
a) Tìm số hạng tổng quát un của dãy số \((u_n)\).
b) Chứng minh rằng \((u_n)\) có giới hạn là 0.
c) Từ kết quả câu b), chứng tỏ rằng sau một số năm nào đó khối lượng chất phóng xạ đã cho ban đầu không còn độc hại đối với con người, cho biết chất phóng xạ này sẽ không độc hại nữa nếu khối lượng chất phóng xạ còn lại bé hơn \(10^{-6} g\).
-
Bài tập 2 trang 121 SGK Đại số & Giải tích 11
Biết dãy số \((u_n )\) thỏa mãn \(|u_n -1| <\frac{1}{n^{3}}\) với mọi n. Chứng minh rằng lim \(u_n =1\).
-
Bài tập 3 trang 121 SGK Đại số & Giải tích 11
Tìm giới hạn sau:
a) \(lim\frac{6n - 1}{3n +2}\);
b) \(lim\frac{3n^{2}+n-5}{2n^{2}+1}\);
c) \(lim\frac{3^{n}+5.4^{n}}{4^{n}+2^{n}}\);
d) \(lim\frac{\sqrt{9n^{2}-n+1}}{4n -2}\).
-
Bài tập 4 trang 122 SGK Đại số & Giải tích 11
Để trang hoàng cho căn hộ của mình, chú chuột Mickey quyết định tô màu một miếng bìa hình vuông cạnh bằng 1. Nó tô màu xám các hình vuông nhỏ được đánh dấu 1, 2, 3, ..., n trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó.
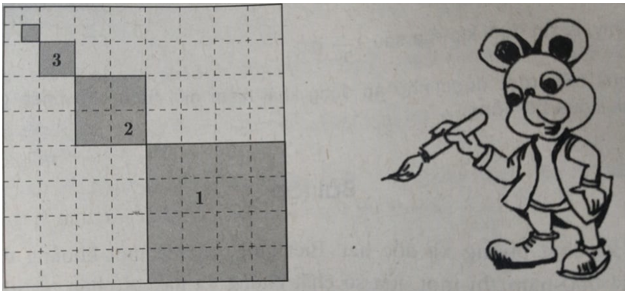
Giả sử quy trình tô màu của Mickey có thể tiến ra vô hạn.
a) Gọi un là diện tích của hình vuông màu xám thứ n. Tính \(u_1 , u_2 , u_3\) và \(u_n\).
b) Tính lim\(S_n\) với \(S_n = u_1 + u_2 + u_3 + ... + u_n\) .
- VIDEOYOMEDIA
-
Bài tập 5 trang 122 SGK Đại số & Giải tích 11
Tính tổng \(S = -1 + \frac{1}{10}-\frac{1}{10^{2}}+...+ \frac{(-1)^{n}}{10^{n-1}}\) + ...
-
Bài tập 6 trang 122 SGK Đại số & Giải tích 11
Cho số thập phân vô hạn tuần hoàn a = 1, 020 020 ... (chu kì là 02). Hãy viết a dưới dạng một phân số.
-
Bài tập 7 trang 122 SGK Đại số & Giải tích 11
Tính các giới hạn sau:
a) \(lim (n^3 + 2n^2 - n + 1)\);
b) \(lim (-n^2 + 5n - 2)\);
c) \(lim(\sqrt{n^{2}-n}-n)\) ;
d) (\(lim(\sqrt{n^{2}-n}+n)\).
-
Bài tập 8 trang 122 SGK Đại số & Giải tích 11
Cho hai dãy số \((u_n)\)và \((v_n)\). Biết \(lim u_n = 3, lim v_n = +\infty .\)
Tính các giới hạn:
a) \(lim\frac{3u_{n}-1}{u_{n}+ 1};\)
b) \(lim\frac{v_{n}+ 2}{v^{2}_{n}-1}\).
-
Bài tập 4.1 trang 156 SBT Toán 11
Biết rằng dãy số () có giới hạn 0. Giải thích vì sao dãy số () với cũng có giới hạn 0. Chiều ngược lại có đúng không?
-
Bài tập 4.2 trang 156 SBT Toán 11
Cho biết dãy số () có giới hạn hữu hạn, còn dãy số () không có giới hạn hữu hạn. Dãy số () có thể có giới hạn hữu hạn không?
-
Bài tập 4.3 trang 156 SBT Toán 11
a) Cho hai dãy số (un) và (v
n ). Biết \(\lim {u_n} = - \infty \) và vn ≤ un với mọi n. Có kết luận gì về giới hạn của dãy (vn) khi \(n \to + \infty \)?b) Tìm vn với vn = - n!
-
Bài tập 4.4 trang 156 SBT Toán 11
Tính giới hạn của các dãy số có số hạng tổng quát sau đây, khi \(n \to \infty \).
-
Bài tập 4.5 trang 156 SBT Toán 11
Tính các giới hạn sau:a) \(\lim ({n^2} + 2n - 5)\)b) \(\lim ( - {n^3} - 3{n^2} - 2)\)c) \(\lim [{4^n} + {( - 2)^n}]\) -
Bài tập 4.6 trang 157 SBT Toán 11
Cho hai dãy số () và (). Chứng minh rằng nếu \(\lim {v_n} = 0\) và \(|{u_n}| \le {v_n}\) với mọi thì \(\lim {u_n} = 0\)
-
Bài tập 4.7 trang 157 SBT Toán 11
Biết \(\left| {{u_n} - 2} \right| \le \frac{1}{3}\). Có kết luận gì về giới hạn của dãy số () ?
-
Bài tập 4.8 trang 157 SBT Toán 11
Cho biết dãy số () xác định bởi công thức truy hồi
\(\left\{ \begin{array}{l}
{u_1} = 2\\
{u_{n + 1}} = \frac{{{u_n} + 1}}{2},\,\,n \ge 1
\end{array} \right.\)Chứng minh (un) có giới hạn hữu hạn khi \(n \to + \infty \). Tìm giới hạn đó.
-
Bài tập 4.9 trang 157 SBT Toán 11
Tính tổng của cấp số nhân lùi vô hạn \(1; - \frac{1}{2};\frac{1}{4}; - \frac{1}{8};...;{\left( { - \frac{1}{2}} \right)^{n - 1}};...\)
-
Bài tập 4.10 trang 157 SBT Toán 11
Tìm số hạng tổng quát của cấp số nhân lùi vô hạn có tổng bằng và công bội \(q = \frac{2}{3}\).
-
Bài tập 4.11 trang 157 SBT Toán 11
Cho dãy số () có số hạng tổng quát là \({b_n} = \sin \alpha + {\sin ^2}\alpha + ... + {\sin ^n}\alpha \) với \(\alpha \ne \frac{\pi }{2} + k\pi \). Tìm giới hạn của ().
-
Bài tập 4.12 trang 157 SBT Toán 11
Cho số thập phân vô hạn tuần hoàn \(a = 34,121212 \ldots \) (chu kì là ). Hãy viết dưới dạng một phân số.
-
Bài tập 4.13 trang 157 SBT Toán 11
Giới hạn của dãy số () với \({u_n} = {( - 1)^n}\) là:
A. 0
B. 1
C. - 1
D. Không tồn tại
-
Bài tập 4.14 trang 157 SBT Toán 11
\(\lim \frac{{{{\left( {2 - 3n} \right)}^2}\left( {n + 1} \right)}}{{1 - 4{n^3}}}\) bằng:
A. \(\frac{3}{4}\)
B. 0
C. \(\frac{9}{4}\)
D. \(-\frac{9}{4}\)
-
Bài tập 4.15 trang 157 SBT Toán 11
\(\lim \left( {\sqrt {{n^2} - 1} - \sqrt {{n^2} + 2} } \right)n\) bằng:A. 0B. - 3C. \( - \frac{3}{2}\)D. \( + \infty \) -
Bài tập 4.16 trang 158 SBT Toán 11
Nếu \(S = 1 + 0,9 + {(0,9)^2} + {(0,9)^3} + ... + {(0,9)^n} + ...\) thì:
A.
B.
C.
D. Không thể tính được
-
Bài tập 4.17 trang 158 SBT Toán 11
\(\lim \frac{{{3^n} - {4^n} + 1}}{{{3^n} + {2^n}}}\) bằng
A. 0
B. \( + \infty \)
C. \(- \infty \)
D. \( - \frac{4}{3}\]
-
Bài tập 1 trang 130 SGK Toán 11 NC
Chứng minh rằng các dãy số với số hạng tổng quát sau đây có giới hạn 0:
a) \(\frac{{{{\left( { - 1} \right)}^n}}}{{n + 5}}\)
b) \(\frac{{\sin n}}{{n + 5}}\)
c) \(\frac{{\cos 2n}}{{\sqrt n + 1}}\)
-
Bài tập 2 trang 130 SGK Toán 11 NC
Chứng minh rằng hai dãy số (un) và (vn) với
\({u_n} = \frac{1}{{n\left( {n + 1} \right)}},\,\,\,{v_n} = \frac{{{{\left( { - 1} \right)}^n}\cos n}}{{{n^2} + 1}}\)
Có giới hạn 0.
-
Bài tập 3 trang 130 SGK Toán 11 NC
Chứng minh rằng các dãy số (un) sau đây có giới hạn 0:
a) \({u_n} = {\left( {0,99} \right)^n}\)
b) \({u_n} = \frac{{{{\left( { - 1} \right)}^n}}}{{{2^n} + 1}}\)
c) \({u_n} = - \frac{{\sin \frac{{n\pi }}{5}}}{{{{\left( {1,01} \right)}^n}}}\)
-
Bài tập 4 trang 130 SGK Toán 11 NC
Cho dãy số (un) với \({u_n} = \frac{n}{{{3^n}}}\)
a. Chứng minh rằng \(\frac{{{u_{n + 1}}}}{{{u_n}}} \le \frac{2}{3}\) với mọi n.
b. Bằng phương pháp qui nạp, chứng minh rằng \(0 < {u_n} \le {\left( {\frac{2}{3}} \right)^n}\) với mọi n.
c. Chứng minh rằng dãy số (un) có giới hạn 0.
-
Bài tập 5 trang 134 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\lim \left( {2 + \frac{{{{\left( { - 1} \right)}^n}}}{{n + 2}}} \right)\)
b) \(\lim \left( {\frac{{\sin 3n}}{{4n}} - 1} \right)\)
c) \(\lim \frac{{n - 1}}{n}\)
d) \(\lim \frac{{n + 2}}{{n + 1}}\)
-
Bài tập 6 trang 134 SGK Toán 11 NC
Tìm \(\lim u_n\) với:
a) \({u_n} = \frac{{{n^2} - 3n + 5}}{{2{n^2} - 1}}\)
b) \({u_n} = \frac{{ - 2{n^2} + n + 2}}{{3{n^4} + 5}}\)
c) \({u_n} = \frac{{\sqrt {2{n^2} - n} }}{{1 - 3{n^2}}}\)
d) \({u_n} = \frac{{{4^n}}}{{{{2.3}^n} + {4^n}}}\)
-
Bài tập 7 trang 135 SGK Toán 11 NC
Cho dãy số (un) xác định bởi
u1 = 10 và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) với mọi n ≥ 1
a. Chứng minh rằng dãy số (vn) xác định bởi \({v_n} = {u_n} - \frac{{15}}{4}\) là một cấp số nhân.
b. Tìm \(\lim u_n\).
-
Bài tập 8 trang 135 SGK Toán 11 NC
Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1 có các đỉnh là trung điểm các cạnh của tam giác ABC, tam giác A2B2C2 có các đỉnh là trung điểm các cạnh của tam giác A1B1C1,…, tam giác An+1Bn+1Cn+1 có các đỉnh là trung điểm các cạnh của tam giác AnBnCn, … . Gọi p1, p2, ..., pn, … và S1, S2, …, Sn, … theo thứ tự là chu vi và diện tích của các tam giác.
a. Tìm giới hạn của các dãy số (pn) và (Sn).
b. Tìm các tổng p1+p2+...+pn+... và S1+S2+...+Sn+...
-
Bài tập 9 trang 135 SGK Toán 11 NC
Biểu diễn các số thập phân vô hạn tuần hoàn sau dưới dạng phân số:
a) 0,444...
b) 0,2121...
c) 0,32111...
-
Bài tập 10 trang 135 SGK Toán 11 NC
Gọi C là nửa đường tròn đường kính AB = 2R, C1 là đường gồm hai nửa đường tròn đường kính \(\frac{{AB}}{2}\), C2 là đường gồm bốn nửa đường tròn đường kính \(\frac{{AB}}{4}\),... Cn là đường gồm 2n nửa đường tròn đường kính \(\frac{{AB}}{{2n}}\),... (h. 4.2). Gọi pn là độ dài của Cn, Sn là diện tích hình phẳng giới hạn bởi Cn và đoạn thẳng AB.
a. Tính pn và Sn.
b. Tìm giới hạn của các dãy số (pn) và (Sn).
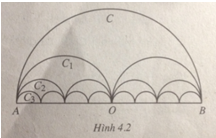
-
Bài tập 11 trang 142 SGK Toán 11 NC
Tìm giới hạn của các dãy số (un) với:
a) \({u_n} = - 2{n^3} + 3n + 5\)
b) \({u_n} = \sqrt {3{n^4} + 5{n^3} - 7n} \)
-
Bài tập 12 trang 142 SGK Toán 11 NC
Tìm giới hạn của các dãy số (un) với:
a) \({u_n} = \frac{{ - 2{n^3} + 3n - 2}}{{3n - 2}}\)
b) \({u_n} = \frac{{\sqrt[3]{{{n^5} - 7{n^3} - 5n + 8}}}}{{n + 12}}\)
-
Bài tập 13 trang 142 SGK Toán 11 NC
Tìm các giới hạn sau:
a. \(lim (2n+\cos n)\)
b. \(\lim \left( {\frac{1}{2}{n^2} - 3\sin 2n + 5} \right)\)
-
Bài tập 14 trang 142 SGK Toán 11 NC
Chứng minh rằng nếu q > 1 thì \(\lim {q^n} = + \infty \).
-
Bài tập 15 trang 142 SGK Toán 11 NC
Tìm giới hạn của các dãy số (un) với:
a) \({u_n} = \frac{{{3^n} + 1}}{{{2^n} - 1}}\)
b) \({u_n} = {2^n} - {3^n}\)
-
Bài tập 16 trang 143 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\lim \frac{{{n^2} + 4n - 5}}{{3{n^3} + {n^2} - 7}}\)
b) \(\lim \frac{{{n^5} + {n^4} - 3n - 2}}{{4{n^3} + 6{n^2} + 9}}\)
c) \(\lim \frac{{\sqrt {2{n^4} + 3n - 2} }}{{2{n^2} - n + 3}}\)
d) \(\lim \frac{{{3^n} - {{2.5}^n}}}{{7 + {{3.5}^n}}}\)
-
Bài tập 17 trang 143 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\lim \left( {3{n^3} - 7n + 11} \right)\)
b) \(\lim \sqrt {2{n^4} - {n^2} + n + 2} \)
c) \(\lim \sqrt[3]{{1 + 2n - {n^3}}}\)
d) \(\lim \sqrt {{{2.3}^n} - n + 2} \)
-
Bài tập 18 trang 143 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\lim \left( {\sqrt {{n^2} + n + 1} - n} \right)\)
Hướng dẫn: Nhân và chia biểu thức đã cho với \({\sqrt {{n^2} + n + 1} + n}\)
b) \(\lim \frac{1}{{\sqrt {n + 2} - \sqrt {n + 1} }}\)
Hướng dẫn: Nhân tử và mẫu của phân thức đã cho với \({\sqrt {n + 2} + \sqrt {n + 1} }\)
c) \(\lim {\rm{ }}\left( {\sqrt {{n^2} + n + 2} - \sqrt {n + 1} } \right)\)
d) \(\lim \frac{1}{{\sqrt {3n + 2} - \sqrt {2n + 1} }}\)
e) \(\lim \left( {\sqrt {n + 1} - \sqrt n } \right)n\)
f) \(\lim \frac{{\sqrt {{n^2} + 1} - \sqrt {n + 1} }}{{3n + 2}}\)
-
Bài tập 19 trang 143 SGK Toán 11 NC
Tổng của một cấp số nhân lùi vô hạn là \(\frac{5}{3}\), tổng ba số hạng đầu tiên của nó là \(\frac{{39}}{{25}}\). Tìm số hạng đầu và công bội của cấp số đó.
-
Bài tập 20 trang 143 SGK Toán 11 NC
Bông tuyết Vôn Kốc
Ta bắt đầu từ một tam giác đều cạnh a. Chia mỗi cạnh của tam giác ABC thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài tam giác ABC rồi xóa đáy của nó, ta được đường gấp khúc khép kín H1. Chia mỗi cạnh H1 thành ba đoạn thẳng bằng nhau. Trên mỗi đoạn thẳng ở giữa, dựng một tam giác đều nằm ngoài H1 rồi xóa đáy của nó, ta được đường gấp khúc khép kín H2. Tiếp tục như vậy, ta được một hình giống như bông tuyết, gọi là bông tuyết Vôn Kốc (h. 4.6).
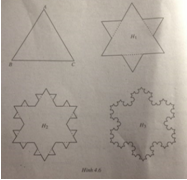
a. Gọi p1, p2, … , pn, … là độ dài của H1, H2, … , Hn, … . Chứng minh rằng (pn) là một cấp số nhân. Tìm \(\lim p_n\).
b. Gọi Sn là diện tích của miền giới hạn bởi đường gấp khúc Hn. Tính Sn và tìm giới hạn của dãy số (Sn).
Hướng dẫn: Số cạnh của Hn là 3.4n. Tìm độ dài mỗi cạnh của Hn, từ đó tính pn. Để tính Sn cần chú ý rằng muốn có Hn+1 chỉ cần thêm vào một tam giác đều nhỏ trên mỗi cạnh của Hn.





