Bài tập 7 trang 135 SGK Toán 11 NC
Cho dãy số (un) xác định bởi
u1 = 10 và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) và \({u_{n + 1}} = \frac{{{u_n}}}{5} + 3\) với mọi n ≥ 1
a. Chứng minh rằng dãy số (vn) xác định bởi \({v_n} = {u_n} - \frac{{15}}{4}\) là một cấp số nhân.
b. Tìm \(\lim u_n\).
Hướng dẫn giải chi tiết
a) Ta có \({v_{n + 1}} = {u_{n + 1}} - \frac{{15}}{4} = \frac{{{u_n}}}{5} + 3 - \frac{{15}}{4} = \frac{{{u_n}}}{5} - \frac{3}{4}\)
Thay \({u_n} = {v_n} + \frac{{15}}{4}\) vào ta được:
\({v_{n + 1}} = \frac{1}{5}\left( {{v_n} + \frac{{15}}{4}} \right) - \frac{3}{4} = \frac{1}{5}{v_n},\forall n\)
Vậy (vn) là cấp số nhân lùi vô hạn với công bội \(q = \frac{1}{5}\)
b)
\(\begin{array}{l}
{v_1} = {u_1} - \frac{{15}}{4} = 10 - \frac{{15}}{4} = \frac{{25}}{4}\\
{v_n} = {v_1}.{q^{n - 1}} = \frac{{25}}{4}.{\left( {\frac{1}{5}} \right)^{n - 1}}\\
\Rightarrow \lim {v_n} = 0 \Rightarrow \lim {u_n} = \frac{{15}}{4}
\end{array}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC
-
Câu 37 ạ
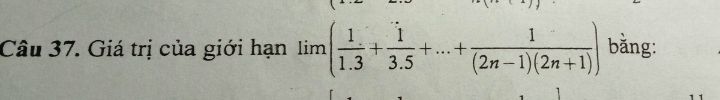Theo dõi (0) 3 Trả lời -
Giá trị của giới hạn lim căn bậc 3(n^2--n^3+n)?
bởi Ziii
15/02/2020
Giúp mình câu 63 với ạ
Theo dõi (0) 2 Trả lời -
Tìm lim u_n biết u_n=1/(2^2-1)+1/(3^2-1)+...+1/(n^2-1)
bởi Trí Trọng
15/02/2020
giải hộ mình nhé
Theo dõi (1) 1 Trả lời -
Chọn mệnh đề đúng trong các mệnh đề sau
bởi Nguyễn Hồng Sơn
15/02/2020
GIỚI HẠN CỦA DÃY SỐ
Câu 1. Chọn mệnh đề đúng trong các mệnh đề sau:
A. Nếu
, thì 
. B. Nếu , thì 
.C. Nếu
, thì 
. D. Nếu 
, thì 
.Câu 2. Giá trị của
bằng:A. 0 B. 1 C. 2 D. 3Câu 3. Giá trị của
bằng: A. 0 B. 2 C. 4 D. 5Câu 4. Giá trị của
bằng: A. 0 B. 3 C. 5 D. 8Câu 5. Giá trị của
bằng: A. 
B. 
C. 0 D. 
Câu 6. Giá trị của
bằng: A. B. C. 0 D. Câu 7. Giá trị của
bằng: A. B. C. 0 D. Câu 8. Giá trị của
bằng: A. B. C. 0 D. Câu 9. Giá trị của
bằng: A. B. C. 0 D. Câu 10. Giá trị của
bằng: A. B. C. 0 D. Câu 11. Giá trị của
bằng: A. B. C. 0 D. Câu 12. Giá trị của
bằng: A. B. C. 2 D. Câu 13. Giá trị của
bằng: A. B. C. 0 D. Câu 14. Giá trị của
bằng: A. B. C. 0 D. Câu 15. Giá trị của
bằng: A. B. C. 
D. Câu 16. Giá trị của
bằng: A. B. C. 
D. Câu 17. Giá trị của
bằng: A. B. C. 0 D. Câu 18. Giá trị của
bằng: A. B. C. 0 D. 4Câu 19. Giá trị của
bằng: A. B. C. 0 D. Câu 20. Giá trị của
với 
bằng:A. B. C. 0 D. Câu 1. Cho dãy số
với 
và 
. Chọn giá trị đúng của 
trong các số sau:A.
. B. . C. 
. D. .Câu 2. Kết quả đúng của
là: A. 4. B. 5. C. –4. D. 
.Câu 3. Giá trị của.
bằng: A. B. C. 
D. Câu 4. Giá trị của.
bằng: A. B. C. 
D. Theo dõi (0) 0 Trả lời -
ADMICRO
Tính lim căn(n^4+3n-2)/(2n^2-n+3)
bởi Ngân Hà
14/02/2020
Theo dõi (0) 0 Trả lời
