Bài tập 13 trang 142 SGK Toán 11 NC
Tìm các giới hạn sau:
a. \(lim (2n+\cos n)\)
b. \(\lim \left( {\frac{1}{2}{n^2} - 3\sin 2n + 5} \right)\)
Hướng dẫn giải chi tiết
Ta có:
\(\begin{array}{*{20}{l}}
{2n + \cos n = n\left( {2 + \frac{{\cos n}}{n}} \right)}\\
\begin{array}{l}
\left| {\frac{{\cos n}}{n}} \right| \le \frac{1}{n},\lim \frac{1}{n} = 0\\
\Rightarrow \lim \frac{{\cos n}}{n} = 0
\end{array}
\end{array}\)
Do đó \(\lim \left( {2 + \frac{{\cos n}}{n}} \right) = 2 > 0\) và \(\lim n = + \infty \)
Suy ra \(\lim \left( {2n + \cos n} \right) = + \infty \)
b)
\(\begin{array}{l}
\lim \left( {\frac{1}{2}{n^2} - 3\sin 2n + 5} \right)\\
= \lim {n^2}\left( {\frac{1}{2} - \frac{{3\sin 2n}}{{{n^2}}} + \frac{5}{{{n^2}}}} \right) = + \infty
\end{array}\)
(vì \(\lim {n^2} = + \infty ,\lim \left( {\frac{1}{2} - \frac{{3\sin 2n}}{{{n^2}}} + \frac{5}{{{n^2}}}} \right) = \frac{1}{2} > 0\))
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-


Tính lim(7^(n+1)-3^2n)/(3^(2n+1)+7^n)
bởi Thủy Em
 13/01/2020
13/01/2020
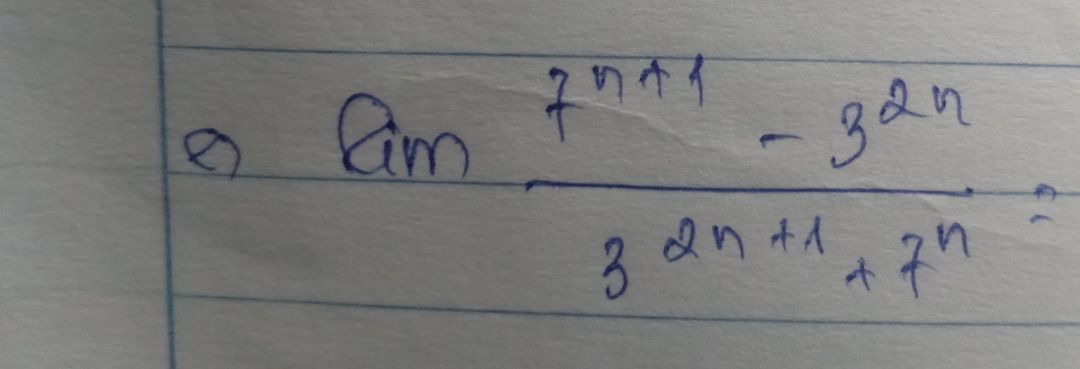 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tìm giới hạn của n(căn(n^2-1)-căn(n^2+2))
bởi Truong Phuong Anh
 12/01/2020
Giải giúp mình vs •~•
12/01/2020
Giải giúp mình vs •~•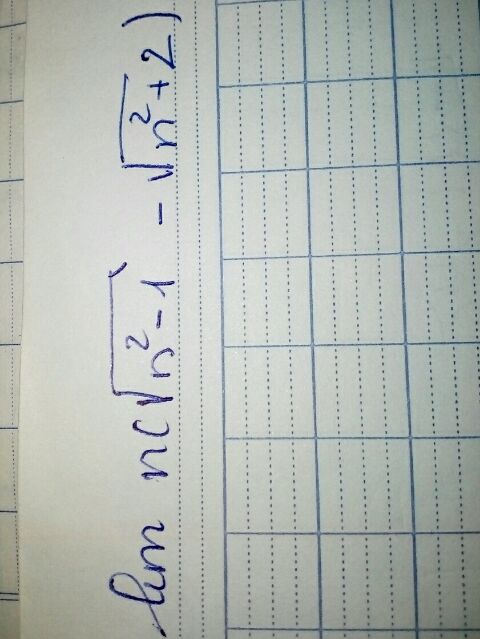 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính lim (1+2+3+...+n)/(2n^2+n+1)
bởi Hoàng Nguyệt
 12/01/2020
12/01/2020
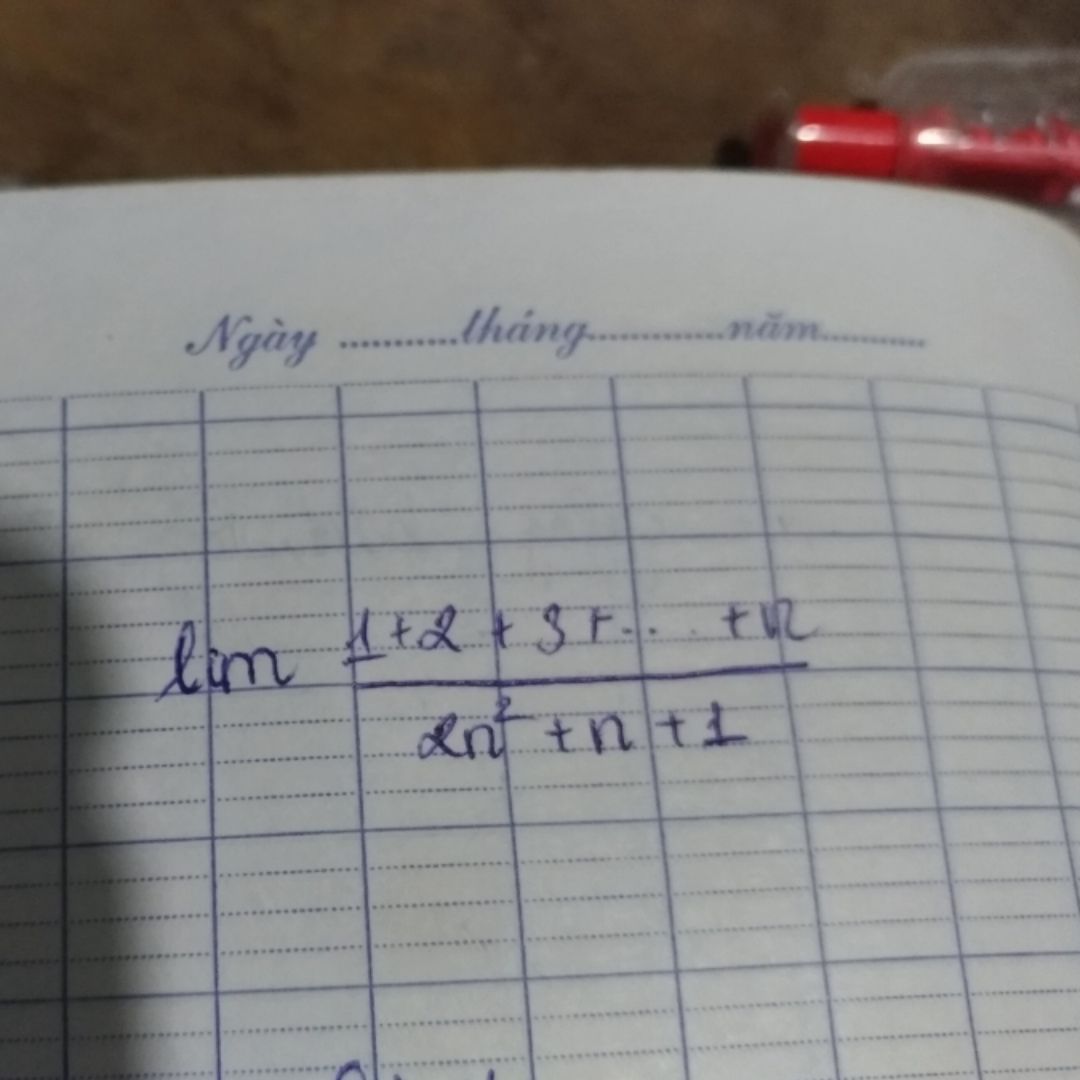 Theo dõi (1) 4 Trả lời
Theo dõi (1) 4 Trả lời -


Tính lim (x-căn(x+2))/căn(4x-3)
bởi Thucky Duong
 12/01/2020
Lim x-căn x 2/ căn 4x-3
12/01/2020
Lim x-căn x 2/ căn 4x-3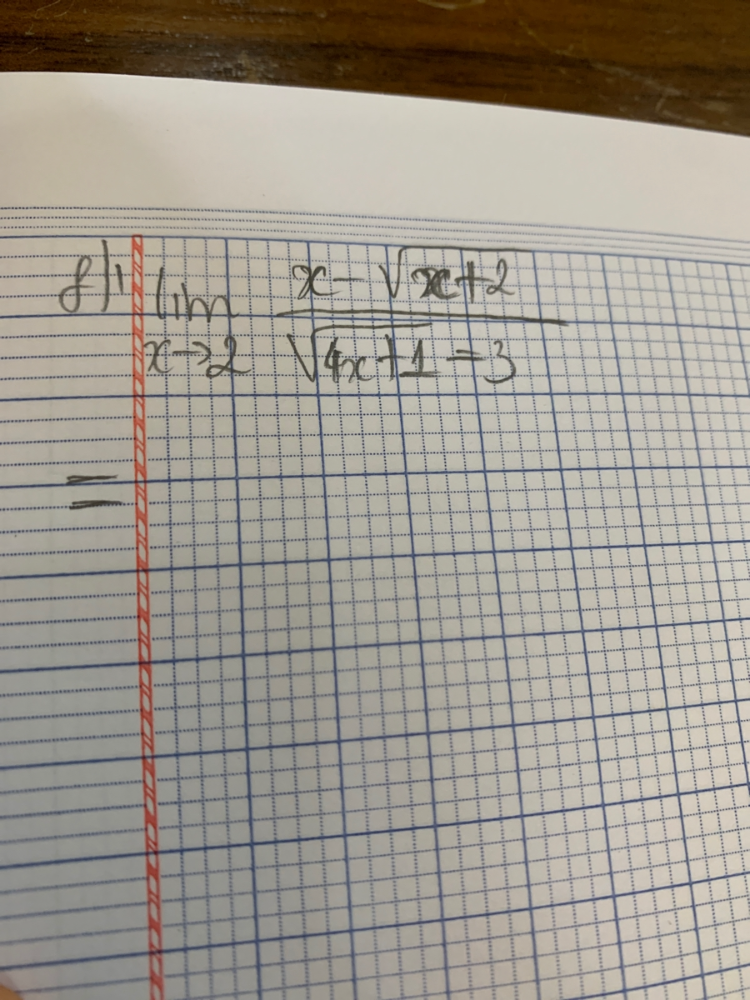 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Tính lim (3^n-4^n+1)/(2.4^n+2^n)
bởi Tôn Thị Thảo Nguyên
 11/01/2020
Tính các giới hạn
11/01/2020
Tính các giới hạn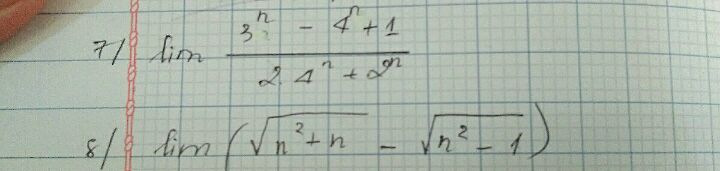 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời





