Giải bài 4.15 tr 157 SBT Toán 11
Hướng dẫn giải chi tiết
\(\begin{array}{l}
lim\left( {\sqrt {{n^2} - 1} - \sqrt {{n^2} + 2} } \right)n = lim\frac{{\left( {{n^2} - 1} \right) - \left( {{n^2} + 2} \right)}}{{\sqrt {{n^2} - 1} + \sqrt {{n^2} + 2} }}\\
= lim\frac{{ - 3n}}{{n\sqrt {1 - \frac{1}{{{n^2}}}} + n\sqrt {1 + \frac{2}{{{n^2}}}} }} = - \frac{3}{2}
\end{array}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 4.13 trang 157 SBT Toán 11
Bài tập 4.14 trang 157 SBT Toán 11
Bài tập 4.16 trang 158 SBT Toán 11
Bài tập 4.17 trang 158 SBT Toán 11
Bài tập 1 trang 130 SGK Toán 11 NC
Bài tập 2 trang 130 SGK Toán 11 NC
Bài tập 3 trang 130 SGK Toán 11 NC
Bài tập 4 trang 130 SGK Toán 11 NC
Bài tập 5 trang 134 SGK Toán 11 NC
Bài tập 6 trang 134 SGK Toán 11 NC
Bài tập 7 trang 135 SGK Toán 11 NC
Bài tập 8 trang 135 SGK Toán 11 NC
Bài tập 9 trang 135 SGK Toán 11 NC
Bài tập 10 trang 135 SGK Toán 11 NC
Bài tập 11 trang 142 SGK Toán 11 NC
Bài tập 12 trang 142 SGK Toán 11 NC
Bài tập 13 trang 142 SGK Toán 11 NC
Bài tập 14 trang 142 SGK Toán 11 NC
Bài tập 15 trang 142 SGK Toán 11 NC
Bài tập 16 trang 143 SGK Toán 11 NC
Bài tập 17 trang 143 SGK Toán 11 NC
Bài tập 18 trang 143 SGK Toán 11 NC
-


Tính giới hạn của (3n^2-2n+5)/(2n^2+5n-3)
bởi Bảo Bình
 31/03/2020
31/03/2020
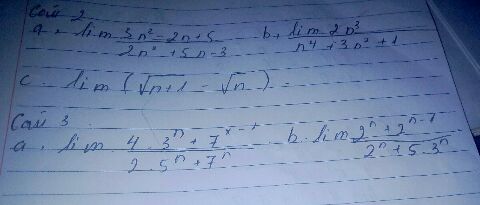 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 Giải giúp em với mn oiw
Giải giúp em với mn oiw Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giới hạn (1+3^n)/(4+3^n)
bởi Nguyễn Trần Tiến
 23/03/2020
Bài tập
23/03/2020
Bài tập Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -
ADMICRO


Tính giới hạn của căn(5n^2+n+1)-2n+3
bởi Phạm Như
 19/03/2020
Giúp mình với
19/03/2020
Giúp mình với Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời





