Giải bài tập SGK Bài 2 Chương 4 Toán 11 Cơ bản & Nâng cao

Dùng định nghĩa tìm các giới hạn sau:

a) \(\underset{x\rightarrow 4}{lim} \ \frac{x+1}{3x - 2}\);

b) \(\underset{x \rightarrow +\infty }{lim}\frac{2-5x^{2}}{x^{2}+3}\).

Cho hàm số \(f(x) =\left\{\begin{matrix} \sqrt{x}+1; &x\geq 0 \\ 2x;& x <0 \end{matrix}\right.\)

và các dãy số \((u_n)\) với  \(u_n =\frac{1}{n}\), \((v_n)\) với \(v_n = -\frac{1}{n}\).

Tính \(lim u_n, lim v_n, lim f (u_n)\)và \(lim (v_n).\)

Từ đó có kết luận gì về giới hạn của hàm số đã cho khi x → 0 ?

Tính các giới hạn sau:

a) \(\underset{x\rightarrow -3}{lim} \frac{x^{2 }-1}{x+1}\);

b) \(\underset{x\rightarrow -2}{lim}\frac{4-x^{2}}{x + 2}\);

c) \(\underset{x\rightarrow 6}{lim} \frac{\sqrt{x + 3}-3}{x-6}\);

d) \(\underset{x\rightarrow +\infty }{lim} \frac{2x-6}{4-x}\);

e) \(\underset{x\rightarrow +\infty }{lim} \frac{17}{x^{2}+1}\);

f) \(\underset{x\rightarrow +\infty }{lim} \frac{-2x^{2}+x -1}{3 +x}\).

Tính các giới hạn sau:

a) \(\underset{x\rightarrow 2}{lim}\frac{3x -5}{(x-2)^{2}}\);

b) \(\underset{x\rightarrow 1^{-}}{lim}\frac{2x -7}{x-1}\);

c) \(\underset{x\rightarrow 1^{+}}{lim}\frac{2x -7}{x-1}\).

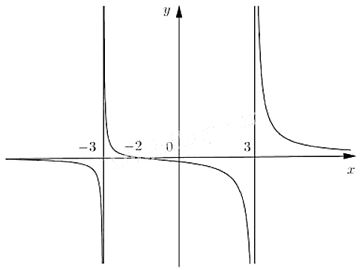
Cho hàm số  \(f(x) =\frac{x+2}{x^{2}-9}\) có đồ thị như hình dưới đây:

a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi \(x \rightarrow -\infty\)

\(x \rightarrow 3^-\) và \(x \rightarrow 3^+\).

b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:

\(\underset{x\rightarrow -\infty }{lim} f(x)\) với f(x) được xét trên khoảng (-3; -3),

\(\underset{x\rightarrow 3^{-}}{lim}f(x)\) với f(x) được xét trên khoảng (-3,3),

\(\underset{x\rightarrow -3^{+}}{lim}f(x)\) với f(x) được xét trên khoảng (-3; 3).

Tính:

a) \(\lim_{+\infty } (x^4 - x^2 + x - 1)\) ;

b) \(\lim_{-\infty } (-2x^3 + 3x^2 -5 )\);

c) \(\lim_{-\infty } \sqrt{x^2-2x+5}\)

d) \(\lim_{+\infty } \frac{\sqrt{x^2+1}+x}{5-2x}\)

Một thấu kính hội tụ có tiêu cự là f. Gọi d và d' lần lượt là khoảng cách từ một vật thật AB và từ ảnh A'B' của nó tới quang tâm O của thấu kính. Công thức thấu kính là \(\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}.\)

a) Tìm biểu thức xác định hàm số d' = f(d).

b) Tìm \(\underset{d\rightarrow f^{+} }{lim}φ(d)\), \(\underset{d\rightarrow f^{-} }{lim}φ(d)\) và \(\underset{d\rightarrow +\infty }{lim}φ(d)\). Giải thích ý nghĩa của các kết quả tìm được.

Dùng định nghĩa tìm các giới hạn

a) \(\mathop {\lim }\limits_{x \to 5} \frac{{x + 3}}{{3 - x}}\)

b) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^3} + 1}}{{{x^2} + 1}}\)

Cho hàm số \(f(x) = \left\{ \begin{array}{l}
{x^2},\,\,\,\,\,\,\,\,\,x \ge 0\\
{x^2} - 1,\,\,x < 0
\end{array} \right.\)

a) Vẽ đồ thị của hàm số f(x). Từ đó dự đoán về giới hạn của f(x) khi x → 0

b) Dùng định nghĩa chứng minh dự đoán trên.

a) Chứng minh rằng hàm số y = sin x không có giới hạn khi \(x \to  + \infty \)$.$

b) Giải thích bằng đồ thị kết luận ở câu a).

Cho hai hàm số y = f(x) và y = g(x) cùng xác định trên khoảng \(( - \infty ;a)\). Dùng định nghĩa chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to  - \infty } f(x) = L\) và \(\mathop {\lim }\limits_{x \to  - \infty } g(x) = M\) thì \(\mathop {\lim }\limits_{x \to  - \infty } f(x).g(x) = L.M\).

Tìm giới hạn của các hàm số sau

a) \(f(x) = \frac{{{x^2} - 2x - 3}}{{x - 1}}\) khi \(x\to 3\)

b) \(h(x) = \frac{{2{x^3} + 15}}{{{{(x + 2)}^2}}}\) khi \(x\to -2\)$\mathrm{}$

c) \(k(x) = \sqrt {4{x^2} - x + 1} \) khi \(x \to  - \infty \)

d) \(h(x) = \frac{{x - 15}}{{x + 2}}\) khi \(x \to  - {2^ + }\) và \(x \to  - {2^ - }\)

Tính giới hạn của các hàm số sau khi \(x \to  - \infty \) và \(x \to  + \infty \)

a) \(f\left( x \right) = \frac{{\sqrt {{x^2} - 3x} }}{{x + 2}}\);

b) \(f(x) = x + \sqrt {{x^2} - x + 1} ;\)

c) \(f\left( x \right) = \sqrt {{x^2} - x}  - \sqrt {{x^2} + 1} \)

Cho khoảng K, x₀ ∈ K và hàm số y = f(x) xác định trên K∖{x₀}.

Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to {x_0}} f(x) =  + \infty \) thì luôn tồn tại ít nhất một số c thuộc K∖{x₀} sao cho f(c) > 0.

Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \((a; + \infty )\)

Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to  + \infty } f(x) =  - \infty \) thì luôn tồn tại ít nhất một số c thuộc \((a; + \infty )\)$$ sao cho \(f\left( c \right){\rm{ }} < {\rm{ }}0\)

\(\mathop {\lim }\limits_{x \to  - \infty } ({x^3} + {x^2} + 1)\) bằng 

A. 1

B. \(+ \infty\)

C. \(- \infty\)

D. - 1

\(\mathop {\lim }\limits_{x \to 0} \frac{{{{(1 + x)}^3} - 1}}{x}\) bằng 

\(\mathop {\lim }\limits_{x \to  - 2} \frac{{\sqrt {{x^2} + 5}  - 3}}{{x + 2}}\) bằng

\(\mathop {\lim }\limits_{x \to  - \infty } \frac{{2{x^4} + 15x + 6}}{{{x^3} - 5x + 2}}\) bằng

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
mx + 2,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \le 1\\
\frac{1}{{x - 1}} - \frac{3}{{{x^3} - 3}},\,x > 1
\end{array} \right.\)

Với giá trị nào của tham số m thì hàm số \(f\left( x \right)\) có giới hạn khi \(x \to 1\)?

Áp dụng định nghĩa giới hạn của hàm số, tìm các giới hạn sau :

a. \(\mathop {\lim }\limits_{x \to  - 1} \frac{{{x^2} - 3x - 4}}{{x + 1}}\)

b. \(\mathop {\lim }\limits_{x \to 1} \frac{1}{{\sqrt {5 - x} }}\)

Cho hàm số \(f\left( x \right) = \cos \frac{1}{x}\) và hai dãy số \(\left( {x{'_n}} \right),\left( {x'{'_n}} \right)\) với:

\(x{'_n} = \frac{1}{{2n\pi }},\,\,\,\,\,\,\,\,\,x'{'_n} = \frac{1}{{\left( {2n + 1} \right)\frac{\pi }{2}}}\)

a. Tìm giới hạn của các dãy số \(\left( {x{'_n}} \right),\left( {x'{'_n}} \right),\left( {f\left( {x{'_n}} \right)} \right)\) và \(\left( {f\left( {x'{'_n}} \right)} \right)\)

b. Tồn tại hay không \(\mathop {\lim }\limits_{x \to 0} \cos \frac{1}{x}\)?

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 2} \left( {3{x^2} + 7x + 11} \right)\)

b) \(\mathop {\lim }\limits_{x \to 1} \frac{{x - {x^3}}}{{\left( {2x - 1} \right)\left( {{x^4} - 3} \right)}}\)

c) \(\mathop {\lim }\limits_{x \to 0} x\left( {1 - \frac{1}{x}} \right)\)

d) \(\mathop {\lim }\limits_{x \to 9} \frac{{\sqrt x  - 3}}{{9x - {x^2}}}\)

e) \(\mathop {\lim }\limits_{x \to \sqrt 3 } \left| {{x^2} - 4} \right|\)

f) \(\mathop {\lim }\limits_{x \to 2} \sqrt {\frac{{{x^4} + 3x - 1}}{{2{x^2} - 1}}} \)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{3{x^2} - x + 7}}{{2{x^3} - 1}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{2{x^4} + 7{x^3} - 15}}{{{x^4} + 1}}\)

c) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {{x^6} + 2} }}{{3{x^3} - 1}}\)

d) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^6} + 2} }}{{3{x^3} - 1}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } \sqrt[3]{{\frac{{{x^2} + 2x}}{{8{x^2} - x + 3}}}}\)

b) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{x\sqrt x }}{{{x^2} - x + 2}}\)

Áp dụng định nghĩa giới hạn bên phải và giới hạn bên trái của hàm số, tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {1^ + }} \sqrt {x - 1} \)

b) \(\mathop {\lim }\limits_{x \to {5^ - }} \left( {\sqrt {5 - x}  + 2x} \right)\)

c) \(\mathop {\lim }\limits_{x \to {3^ + }} \frac{1}{{x - 3}}\)

d) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{1}{{x - 3}}\)

Tìm các giới hạn sau (nếu có):

a. \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{\left| {x - 2} \right|}}{{x - 2}}\)

b. \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{\left| {x - 2} \right|}}{{x - 2}}\)

c. \(\mathop {\lim }\limits_{x \to 2} \frac{{\left| {x - 2} \right|}}{{x - 2}}\) 

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{x + 2\sqrt x }}{{x - \sqrt x }}\)

b) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{4 - {x^2}}}{{\sqrt {2 - x} }}\)

c) \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{{x^2} + 3x + 2}}{{\sqrt {{x^5} + {x^4}} }}\)

d) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{\sqrt {{x^2} - 7x + 12} }}{{\sqrt {9 - {x^2}} }}\)

Cho hàm số

\(f\left( x \right) = \left\{ \begin{array}{l}
2\left| x \right| - 1\,\,\,\,\,\,\,\,khi\,\,x \le  - 2\\
\sqrt {2{x^2} + 1} \,\,\,\,khi\,\,x >  - 2
\end{array} \right.\)

Tìm \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} f\left( x \right),\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to  - 2} f\left( x \right)\) (nếu có).

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to \sqrt 3 } \left| {{x^2} - 8} \right|\)

b) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^2} + x + 1}}{{{x^2} + 2x}}\)

c) \(\mathop {\lim }\limits_{x \to  - 1} \sqrt {\frac{{{x^3}}}{{{x^2} - 3}}} \)

d) \(\mathop {\lim }\limits_{x \to 3} \sqrt[3]{{\frac{{2x\left( {x + 1} \right)}}{{{x^2} - 6}}}}\)

e) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{\sqrt {1 - {x^3}}  - 3x}}{{2{x^2} + x - 3}}\)

f) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{2\left| {x + 1} \right| - 5\sqrt {{x^2} - 3} }}{{2x + 3}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \sqrt 2 } \frac{{{x^3} + 2\sqrt 2 }}{{{x^2} - 2}}\)

b) \(\mathop {\lim }\limits_{x \to 3} \frac{{{x^4} - 27x}}{{2{x^2} - 3x - 9}}\)

c) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{{x^4} - 16}}{{{x^2} + 6x + 8}}\)

d) \(\mathop {\lim }\limits_{x \to {1^ - }} \frac{{\sqrt {1 - x}  + x - 1}}{{\sqrt {{x^2} - {x^3}} }}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \sqrt[3]{{\frac{{2{x^5} + {x^3} - 1}}{{\left( {2{x^2} - 1} \right)\left( {{x^3} + x} \right)}}}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{2\left| x \right| + 3}}{{\sqrt {{x^2} + x + 5} }}\)

c) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^2} + x}  + 2x}}{{2x + 3}}\)

d) \(\mathop {\lim }\limits_{x \to  + \infty } \left( {x + 1} \right)\sqrt {\frac{x}{{2{x^4} + {x^2} + 1}}} \)

Cho hàm số 

\(f\left( x \right) = \left\{ \begin{array}{l}
{x^2} - 2x + 3,\,\,\,x \le 2\\
4x - 3,\,\,\,\,\,\,\,\,\,\,\,\,\,x > 2
\end{array} \right.\)

Tìm \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right),\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right)\) và \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\) (nếu có)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } \left( {3{x^3} - 5{x^2} + 7} \right)\)

b) \(\mathop {\lim }\limits_{x \to  + \infty } \sqrt {2{x^4} - 3x + 12} \)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{2x + 1}}{{x - 2}}\)

b) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{2x + 1}}{{x - 2}}\)

c) \(\mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{x} - \frac{1}{{{x^2}}}} \right)\)

d) \(\mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{1}{{x - 2}} - \frac{1}{{{x^2} - 4}}} \right)\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^3} - 5}}{{{x^2} + 1}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^4} - x} }}{{1 - 2x}}\)

Tính:

a) \(\mathop {\lim }\limits_{x \to 1} \left[ {\frac{2}{{{{\left( {x - 1} \right)}^2}}}.\frac{{2x + 1}}{{2x - 3}}} \right]\)

b) \(\mathop {\lim }\limits_{x \to 1} \frac{5}{{\left( {x - 1} \right)\left( {{x^2} - 3x + 2} \right)}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 2} \frac{{{x^3} - 8}}{{{x^2} - 4}}\)

b) \(\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ + }} \frac{{2{x^2} + 5x - 3}}{{{{\left( {x + 3} \right)}^2}}}\)

c) \(\mathop {\lim }\limits_{x \to {{\left( { - 3} \right)}^ - }} \frac{{2{x^2} + 5x - 3}}{{{{\left( {x + 3} \right)}^2}}}\)

d) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^3} + 1}  - 1}}{{{x^2} + x}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{2{x^2} + x - 10}}{{9 - 3{x^3}}}\)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {2{x^2} - 7x + 12} }}{{3\left| x \right| - 17}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \left( {{x^3} + 1} \right)\sqrt {\frac{x}{{{x^2} - 1}}} \)

b) \(\mathop {\lim }\limits_{x \to  + \infty } \left( {x + 2} \right)\sqrt {\frac{{x - 1}}{{{x^3} + x}}} \)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} + 1}  - x} \right)\)

b) \(\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt {2x - {x^2}}  - 1}}{{{x^2} - x}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{x} + \frac{1}{{{x^2}}}} \right)\)

b) \(\mathop {\lim }\limits_{x \to  - 2} \frac{{{x^3} + 8}}{{x + 2}}\)

c) \(\mathop {\lim }\limits_{x \to 9} \frac{{3 - \sqrt x }}{{9 - x}}\)

d) \(\mathop {\lim }\limits_{x \to 0} \frac{{2 - \sqrt {4 - x} }}{x}\)

e) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{{x^4} - {x^3} + 11}}{{2x - 7}}\)

f) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\sqrt {{x^4} + 4} }}{{x + 4}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \sqrt 3 } \frac{{{x^3} + 3\sqrt 3 }}{{3 - {x^2}}}\)

b) \(\mathop {\lim }\limits_{x \to 4} \frac{{\sqrt x  - 2}}{{{x^2} - 4x}}\)

c) \(\mathop {\lim }\limits_{x \to {1^ + }} \frac{{\sqrt {x - 1} }}{{{x^2} - x}}\)

d) \(\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {{x^2} + x + 1}  - 1}}{{3x}}\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to  - \infty } x\sqrt {\frac{{2{x^3} + x}}{{{x^5} - {x^2} + 3}}} \)

b) \(\mathop {\lim }\limits_{x \to  - \infty } \frac{{\left| x \right| + \sqrt {{x^2} + x} }}{{x + 10}}\)

c) \(\mathop {\lim }\limits_{x \to  + \infty } \frac{{\sqrt {2{x^4} + {x^2} - 1} }}{{1 - 2x}}\)

d) \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {2{x^2} + 1}  + x} \right)\)

Tìm các giới hạn sau:

a) \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt {{x^2} + x}  - \sqrt x }}{{{x^2}}}\)

b) \(\mathop {\lim }\limits_{x \to {1^ - }} x.\frac{{\sqrt {1 - x} }}{{2\sqrt {1 - x}  + 1 - x}}\)

c) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{3 - x}}{{\sqrt {27 - {x^3}} }}\)

d) \(\mathop {\lim }\limits_{x \to {2^ + }} \frac{{\sqrt {{x^3} - 8} }}{{{x^2} - 2x}}\)