Bài tập 28 trang 158 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{x + 2\sqrt x }}{{x - \sqrt x }}\)
b) \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{4 - {x^2}}}{{\sqrt {2 - x} }}\)
c) \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{{x^2} + 3x + 2}}{{\sqrt {{x^5} + {x^4}} }}\)
d) \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{\sqrt {{x^2} - 7x + 12} }}{{\sqrt {9 - {x^2}} }}\)
Hướng dẫn giải chi tiết
a) Với x > 0, ta có: \(\frac{{x + 2\sqrt x }}{{x - \sqrt x }} = \frac{{\sqrt x \left( {\sqrt x + 2} \right)}}{{\sqrt x \left( {\sqrt x - 1} \right)}} = \frac{{\sqrt x + 2}}{{\sqrt x - 1}}\)
Do đó \(\mathop {\lim }\limits_{x \to {0^ + }} \frac{{x + 2\sqrt x }}{{x - \sqrt x }} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt x + 2}}{{\sqrt x - 1}} = \frac{2}{{ - 1}} = - 2\)
b) Với x < 2, ta có: \(\frac{{4 - {x^2}}}{{\sqrt {2 - x} }} = \frac{{\left( {2 - x} \right)\left( {2 + x} \right)}}{{\sqrt {2 - x} }} = \left( {x + 2} \right)\sqrt {2 - x} \)
Do đó \(\mathop {\lim }\limits_{x \to {2^ - }} \frac{{4 - {x^2}}}{{\sqrt {2 - x} }} = \mathop {\lim }\limits_{x \to {2^ - }} \left( {x + 2} \right)\sqrt {2 - x} = 0\)
c) Với x > - 1, ta có:
\(\begin{array}{l}
\frac{{{x^2} + 3x + 2}}{{\sqrt {{x^5} + {x^4}} }} = \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{{x^2}\sqrt {x + 1} }}\\
= \frac{{\sqrt {x + 1} \left( {x + 2} \right)}}{{{x^2}}}
\end{array}\)
Do đó \(\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{{x^2} + 3x + 2}}{{\sqrt {{x^5} + {x^4}} }} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{\sqrt {x + 1} \left( {x + 2} \right)}}{{{x^2}}} = 0\)
d) Với - 3 < x < 3, ta có: \(\frac{{\sqrt {{x^2} - 7x + 12} }}{{\sqrt {9 - {x^2}} }} = \frac{{\sqrt {\left( {3 - x} \right)\left( {4 - x} \right)} }}{{\sqrt {\left( {3 - x} \right)\left( {3 + x} \right)} }} = \frac{{\sqrt {4 - x} }}{{\sqrt {3 + x} }}\)
Do đó \(\mathop {\lim }\limits_{x \to {3^ - }} \frac{{\sqrt {{x^2} - 7x + 12} }}{{\sqrt {9 - {x^2}} }} = \mathop {\lim }\limits_{x \to {3^ - }} \frac{{\sqrt {4 - x} }}{{\sqrt {3 + x} }} = \frac{{\sqrt 6 }}{6}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 26 trang 158 SGK Toán 11 NC
Bài tập 27 trang 158 SGK Toán 11 NC
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC
-


Tính limx→2 (2- căn x+2 /x2-3x+2)
bởi Liên Mỹ
 17/03/2020
17/03/2020
limx→2 (2- căn x+2 /x2-3x+2)
Theo dõi (0) 1 Trả lời -


Tính giới hạn
bởi Đỗ Văn Tuyến
 16/03/2020
Ý (h) ạ
16/03/2020
Ý (h) ạ Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm giới hạn khi x tiến đến a
bởi Nguyễn Thị Trà
 16/03/2020
16/03/2020
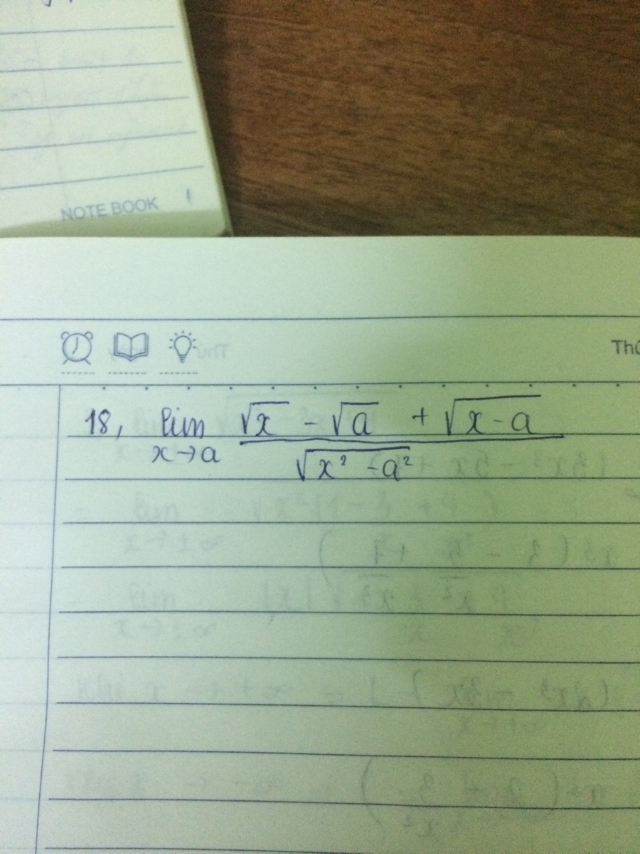 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính giới hạn
bởi Thanh Hiếu
 16/03/2020
16/03/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Tìm giới hạn bằng định nghĩa
bởi Đào Anh
 16/03/2020
Giải giúp mình
16/03/2020
Giải giúp mình Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính limx->1(2x^2 x-3)/x-1
bởi Đào Anh
 16/03/2020
Giải giúp mìnhTheo dõi (0) 3 Trả lời
16/03/2020
Giải giúp mìnhTheo dõi (0) 3 Trả lời -


Tính giới hạn
bởi Chanh Huyenchanh
 16/03/2020
16/03/2020
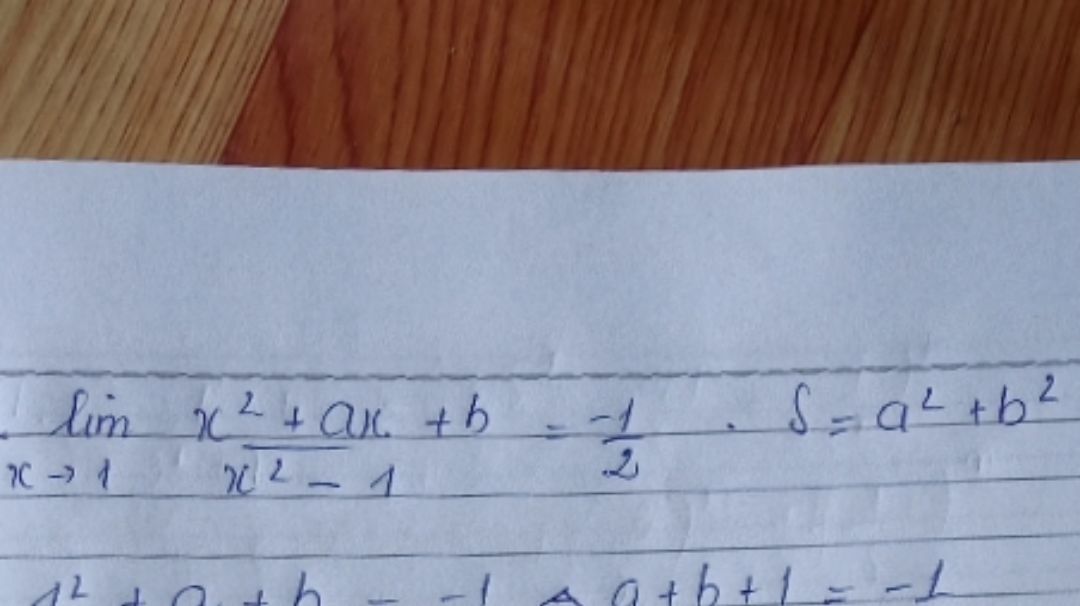 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời


