Bài tập 34 trang 163 SGK Toán 11 NC
Tìm các giới hạn sau:
a) \(\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^3} - 5{x^2} + 7} \right)\)
b) \(\mathop {\lim }\limits_{x \to + \infty } \sqrt {2{x^4} - 3x + 12} \)
Hướng dẫn giải chi tiết
a)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to - \infty } \left( {3{x^3} - 5{x^2} + 7} \right)\\
= \mathop {\lim }\limits_{x \to - \infty } {x^3}\left( {3 - \frac{5}{x} + \frac{7}{{{x^3}}}} \right) = - \infty
\end{array}\)
(vì \(\mathop {\lim }\limits_{x \to - \infty } {x^3} = - \infty ,\mathop {\lim }\limits_{x \to - \infty } \left( {3 - \frac{5}{x} + \frac{7}{{{x^3}}}} \right) = 3 > 0\))
b)
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to + \infty } \sqrt {2{x^4} - 3x + 12} \\
= \mathop {\lim }\limits_{x \to + \infty } {x^2}\sqrt {2 - \frac{3}{{{x^3}}} + \frac{{12}}{{{x^4}}}} = + \infty
\end{array}\)
(vì \(\mathop {\lim }\limits_{x \to + \infty } {x^2} = + \infty ,\mathop {\lim }\limits_{x \to + \infty } \sqrt {2 - \frac{3}{{{x^3}}} + \frac{{12}}{{{x^4}}}} = \sqrt 2 > 0\)).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC
-


Tính lim |x-3|/(3x-6) khi x tiến tới 3+
bởi Hương Mai
 12/02/2020
12/02/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính lim (x^3-x^2+x-1)/(x-1) khi x tiến tới 1
bởi Máy Tính
 12/02/2020
12/02/2020
Ai giúp mình giải 3 câu này với ạ! Mình cảm ơn
lĩm->1 : x^3-x^2+x-1/x-1
lim->-1 : 2x^2+3x+1/x^2+1
lim->a : x^4-a^4/2x-a
Theo dõi (0) 3 Trả lời -


Tính lim (căn bậc 3(2n-n^3)+n-1)
bởi Ly Trần Hải
 10/02/2020
Làm giùm e vs ạ
10/02/2020
Làm giùm e vs ạ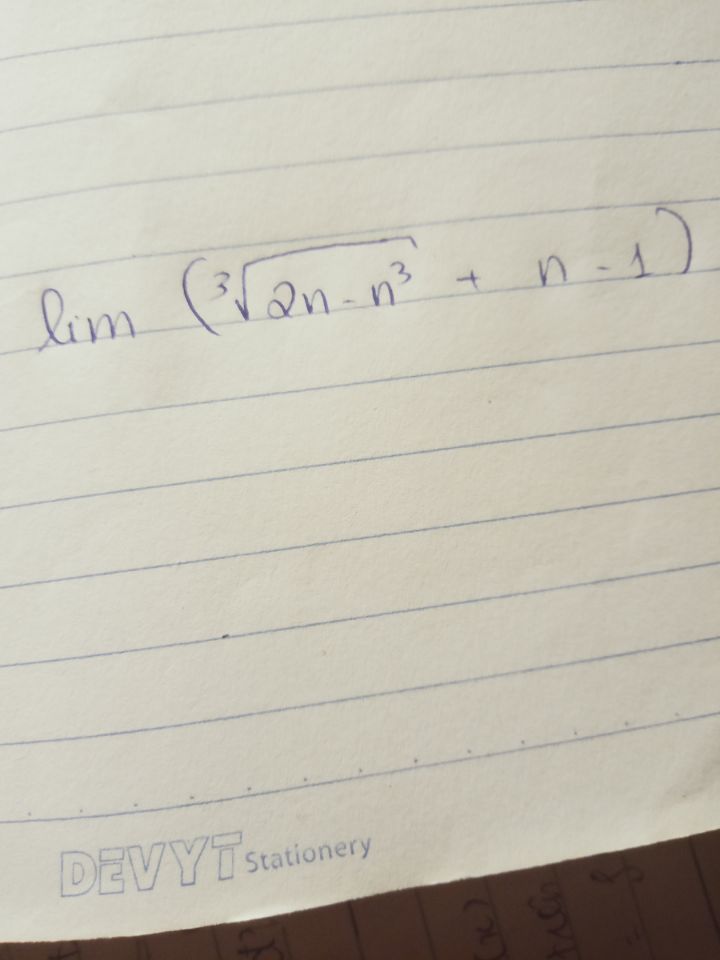 Theo dõi (1) 8 Trả lời
Theo dõi (1) 8 Trả lời -


Tính lim (x^2-4)/(x^2-3x+2) khi x tiến tới 2
bởi Nhock Trương
 10/02/2020
Giải hộ e với ạ
10/02/2020
Giải hộ e với ạ Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -
ADMICRO

 Mn cho e lời giải vs ạ
Mn cho e lời giải vs ạ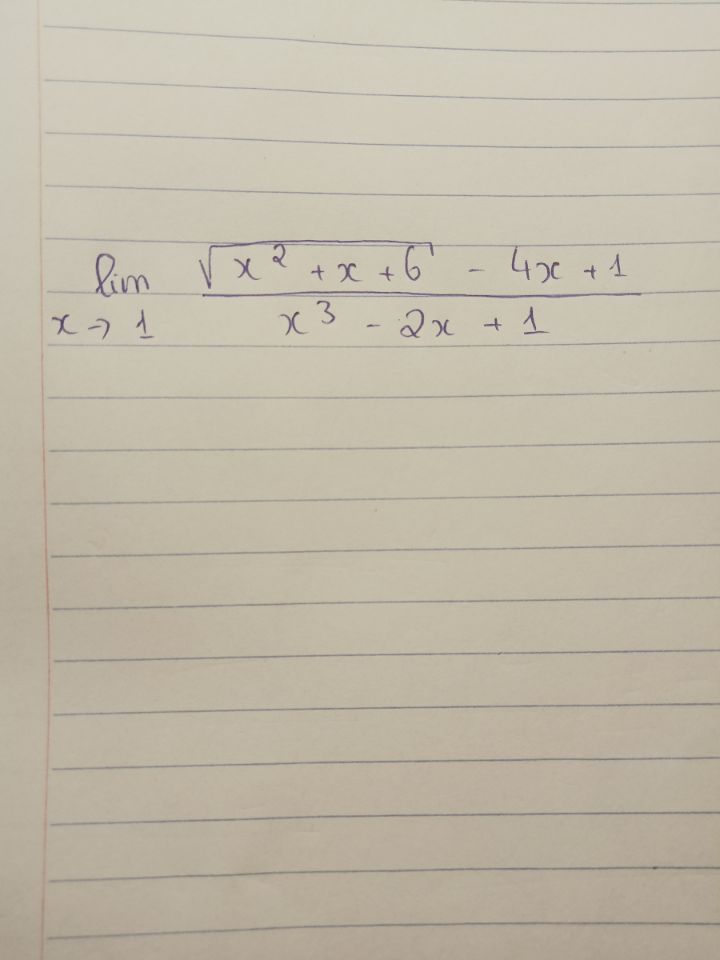 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính lim (x^3-3x+2)/(x^4-4x+3)
bởi Ly Trần Hải
 10/02/2020
Cho mk hỏi tại sao từ đầu lại ra đc bước 2 vậy ạ
10/02/2020
Cho mk hỏi tại sao từ đầu lại ra đc bước 2 vậy ạ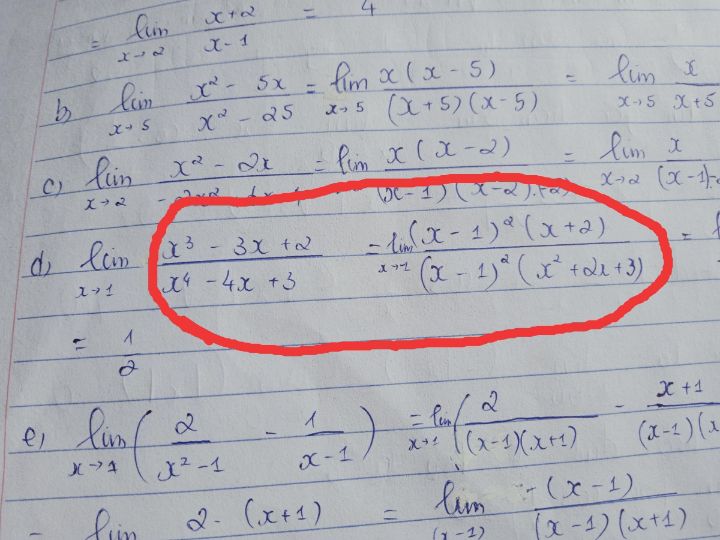 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời


