Giải bài 5 tr 133 sách GK Toán ĐS & GT lớp 11
Cho hàm số \(f(x) =\frac{x+2}{x^{2}-9}\) có đồ thị như hình dưới đây:
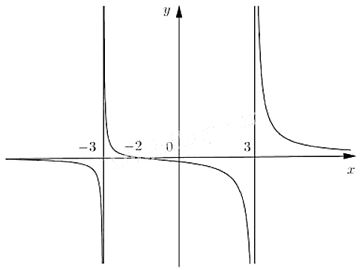
a) Quan sát đồ thị và nêu nhận xét về giá trị hàm số đã cho khi \(x \rightarrow -\infty\)
\(x \rightarrow 3^-\) và \(x \rightarrow 3^+\).
b) Kiểm tra các nhận xét trên bằng cách tính các giới hạn sau:
\(\underset{x\rightarrow -\infty }{lim} f(x)\) với f(x) được xét trên khoảng (-3; -3),
\(\underset{x\rightarrow 3^{-}}{lim}f(x)\) với f(x) được xét trên khoảng (-3,3),
\(\underset{x\rightarrow -3^{+}}{lim}f(x)\) với f(x) được xét trên khoảng (-3; 3).
Hướng dẫn giải chi tiết bài 5
Câu a:
Nhìn vào đồ thị ta có:
* Khi \(x\rightarrow -\infty\) thì \(f(x)\rightarrow 0.\)
* Khi \(x\rightarrow 3\) thì \(f(x)\rightarrow -\infty .\)
* Khi \(x \rightarrow - 3^+\) thì \(f(x) \rightarrow +\infty .\)
Câu b:
* \(\lim_{x\rightarrow -\infty }f(x)=\lim_{x\rightarrow -\infty }\frac{x+2}{x^2-9} =\lim_{x\rightarrow -\infty }\frac{\frac{1}{x}+\frac{2}{x^2}}{1-\frac{9}{x^2}}=0\)
* \(\lim_{x\rightarrow -3^+ }f(x)=\lim_{x\rightarrow -3^+ }\frac{x+2}{x^2-9}=+\infty\)
* \(\lim_{x\rightarrow 3^- }f(x)=\lim_{x\rightarrow 3^- } \frac{x+2}{x^2-9}=-\infty\)
-- Mod Toán 11 HỌC247
Video hướng dẫn giải bài 5 SGK
Bài tập SGK khác
Bài tập 3 trang 132 SGK Đại số & Giải tích 11
Bài tập 4 trang 132 SGK Đại số & Giải tích 11
Bài tập 6 trang 133 SGK Đại số & Giải tích 11
Bài tập 7 trang 133 SGK Đại số & Giải tích 11
Bài tập 4.18 trang 165 SBT Toán 11
Bài tập 4.19 trang 165 SBT Toán 11
Bài tập 4.20 trang 165 SBT Toán 11
Bài tập 4.21 trang 165 SBT Toán 11
Bài tập 4.22 trang 165 SBT Toán 11
Bài tập 4.23 trang 165 SBT Toán 11
Bài tập 4.24 trang 165 SBT Toán 11
Bài tập 4.25 trang 166 SBT Toán 11
Bài tập 4.26 trang 166 SBT Toán 11
Bài tập 4.27 trang 166 SBT Toán 11
Bài tập 4.28 trang 166 SBT Toán 11
Bài tập 4.29 trang 166 SBT Toán 11
Bài tập 4.30 trang 166 SBT Toán 11
Bài tập 4.31 trang 167 SBT Toán 11
Bài tập 21 trang 151 SGK Toán 11 NC
Bài tập 22 trang 152 SGK Toán 11 NC
Bài tập 23 trang 152 SGK Toán 11 NC
Bài tập 24 trang 152 SGK Toán 11 NC
Bài tập 25 trang 152 SGK Toán 11 NC
Bài tập 26 trang 158 SGK Toán 11 NC
Bài tập 27 trang 158 SGK Toán 11 NC
Bài tập 28 trang 158 SGK Toán 11 NC
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC
-


Biết giới hạn. Tính giá trị biểu thức P = a2 - 2b2
bởi NT Nhàn
 17/03/2021
khó
17/03/2021
khó Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính các giới hạn của hàm số
bởi Mỹ Duyên
 15/03/2021
Giúp vs ạ
15/03/2021
Giúp vs ạ Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tính giới hạn của hàm số lượng giác
bởi Hoa Sen
 13/03/2021
13/03/2021
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm giới hạn lim x-căn x 2/căn 4x 1 -3
bởi Thuy Nguyen
 07/03/2021
tìn giới hạn lim x-căn x 2/căn 4x 1 -3Theo dõi (0) 0 Trả lời
07/03/2021
tìn giới hạn lim x-căn x 2/căn 4x 1 -3Theo dõi (0) 0 Trả lời -
ADMICRO


Tính giới hạn của hàm số
bởi Nhạc Tử Thuần
 04/03/2021
Giúp mình câu 8 với ạ!!
04/03/2021
Giúp mình câu 8 với ạ!! Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính giới hạn của hàm số
bởi thu hoài
 03/03/2021
Giúp em với ạ. Em cảm ơn ạ
03/03/2021
Giúp em với ạ. Em cảm ơn ạ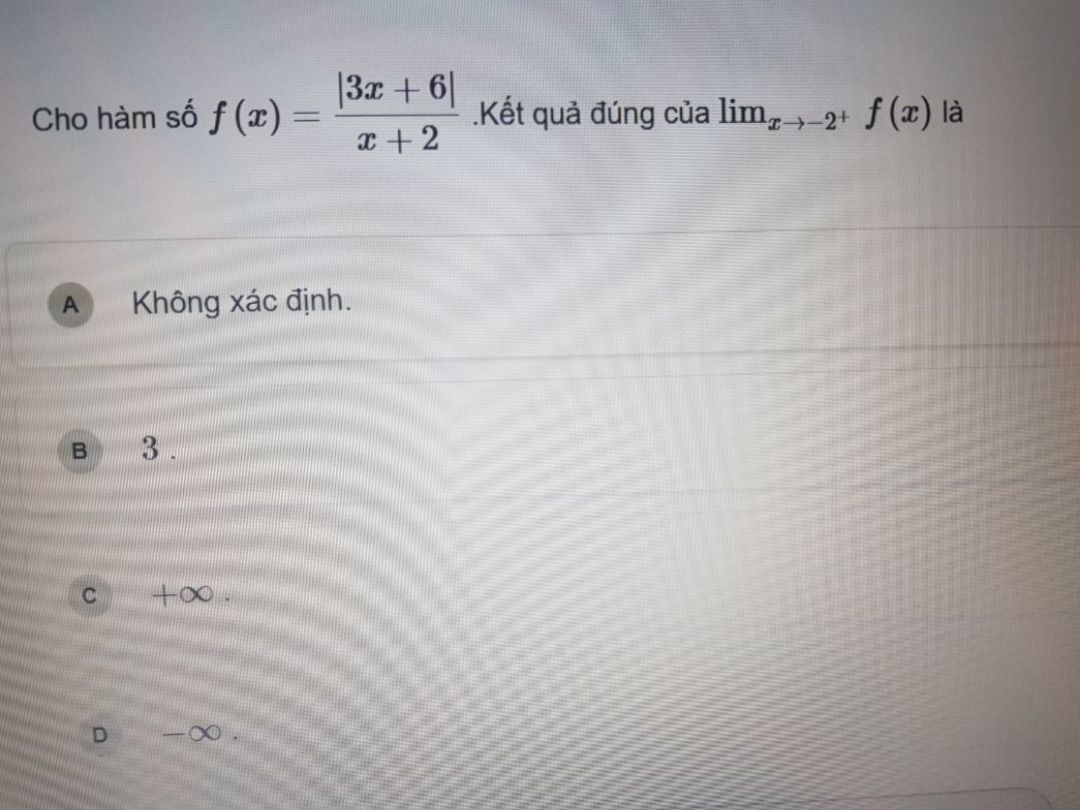 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \(\left( {a; + \infty } \right)\). Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = - \infty \) thì luôn tồn tại ít nhất một số c thuộc \(\left( {a; + \infty } \right)\) sao cho \(f\left( c \right) < 0\)
bởi thuy linh
 28/02/2021
Theo dõi (0) 1 Trả lời
28/02/2021
Theo dõi (0) 1 Trả lời


