Giải bài 4.26 tr 166 SBT Toán 11
Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng \((a; + \infty )\)
Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \) thì luôn tồn tại ít nhất một số c thuộc \((a; + \infty )\) sao cho \(f\left( c \right){\rm{ }} < {\rm{ }}0\)
Hướng dẫn giải chi tiết
Vì \(\mathop {\lim }\limits_{x \to + \infty } f(x) = - \infty \) nên với dãy số bất kì, \({x_n} > a\) và \({x_n} \to + \infty \) ta luôn có \(\mathop {\lim }\limits_{x \to + \infty } f\left( {{x_n}} \right) = - \infty \). Do đó \(\mathop {\lim }\limits_{x \to + \infty } \left[ { - f\left( {{x_n}} \right)} \right] = + \infty \)
Từ định nghĩa suy ra \( - f\left( {{x_n}} \right) > 1\) có thể lớn hơn một số dương bất kì, kể từ một số hạng nào đó trở đi.
Nếu số dương này là 1 thì \( - f\left( {{x_n}} \right) > 1\) kể từ một số hạng nào đó trở đi.
Nói cách khác, luôn tồn tại ít nhất một số \({x_k} \in \left( {a; + \infty } \right)\) sao cho \?( hay \(f\left( {{x_k}} \right) < - 1 < 0\).
Đặt \(c = {x_k}\), ta có \(f\left( c \right){\rm{ }} < {\rm{ }}0\).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 4.24 trang 165 SBT Toán 11
Bài tập 4.25 trang 166 SBT Toán 11
Bài tập 4.27 trang 166 SBT Toán 11
Bài tập 4.28 trang 166 SBT Toán 11
Bài tập 4.29 trang 166 SBT Toán 11
Bài tập 4.30 trang 166 SBT Toán 11
Bài tập 4.31 trang 167 SBT Toán 11
Bài tập 21 trang 151 SGK Toán 11 NC
Bài tập 22 trang 152 SGK Toán 11 NC
Bài tập 23 trang 152 SGK Toán 11 NC
Bài tập 24 trang 152 SGK Toán 11 NC
Bài tập 25 trang 152 SGK Toán 11 NC
Bài tập 26 trang 158 SGK Toán 11 NC
Bài tập 27 trang 158 SGK Toán 11 NC
Bài tập 28 trang 158 SGK Toán 11 NC
Bài tập 29 trang 159 SGK Toán 11 NC
Bài tập 30 trang 159 SGK Toán 11 NC
Bài tập 31 trang 159 SGK Toán 11 NC
Bài tập 32 trang 159 SGK Toán 11 NC
Bài tập 33 trang 159 SGK Toán 11 NC
Bài tập 34 trang 163 SGK Toán 11 NC
Bài tập 35 trang 163 SGK Toán 11 NC
Bài tập 36 trang 163 SGK Toán 11 NC
Bài tập 37 trang 163 SGK Toán 11 NC
Bài tập 38 trang 166 SGK Toán 11 NC
Bài tập 39 trang 166 SGK Toán 11 NC
Bài tập 40 trang 166 SGK Toán 11 NC
Bài tập 41 trang 166 SGK Toán 11 NC
Bài tập 42 trang 167 SGK Toán 11 NC
Bài tập 43 trang 167 SGK Toán 11 NC
-


Tính \(\mathop {\lim }\limits_{x \to \frac{1}{2}} \frac{{8{x^2} - 1}}{{6{x^2} - 5x + 1}}\)?
bởi Anh Hạ
 08/05/2020
08/05/2020
Giúp mình câu d,g,h với
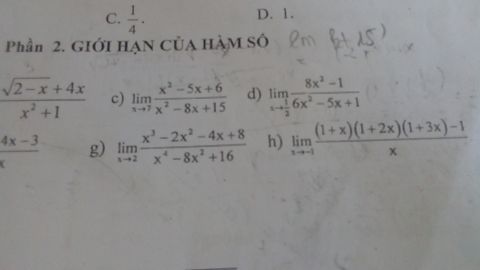 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


1/4 là kết quả của giới hạn nào
bởi Nguyễn Hồng Hân
 04/05/2020
04/05/2020
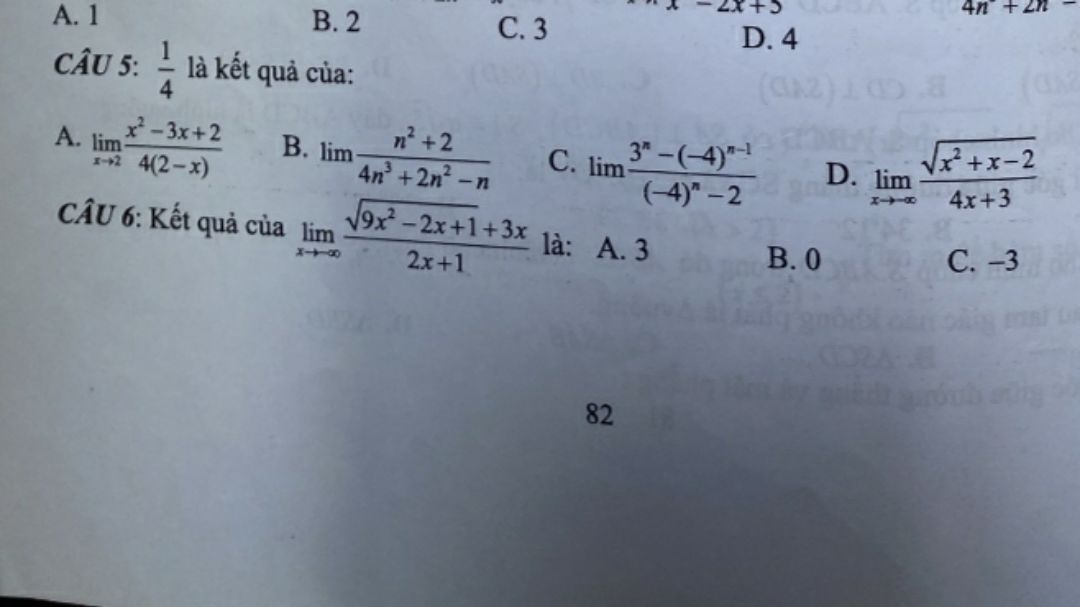 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tính các giới hạn
bởi Nguyễn Văn Khánh
 28/04/2020
giải hộ em ạ
28/04/2020
giải hộ em ạ Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Lim x=>- vo cựccăn 9x2-2x +căn 4x^2+1/ 4x+3
bởi Huệ Tâm
 27/04/2020
27/04/2020
 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -
ADMICRO


Tính \(\mathop {\lim }\limits_{x \to 3} \frac{{x - 3}}{{{x^2} + 2x - 15}}\)?
bởi Nhuu Nguye Quynh
 24/04/2020
24/04/2020
Mọi người giải dùm mình với ạ
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giúp mk câu 4 vs mk c.ơn nhiều
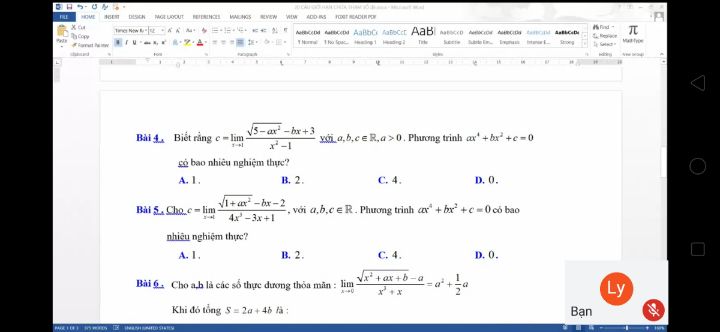 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính giới hạn limx->2 (căn (4x+1)-3)/(x^2-4)
bởi Phạm Thanh Ngân
 23/04/2020
Tính các giới hạn sau??
23/04/2020
Tính các giới hạn sau??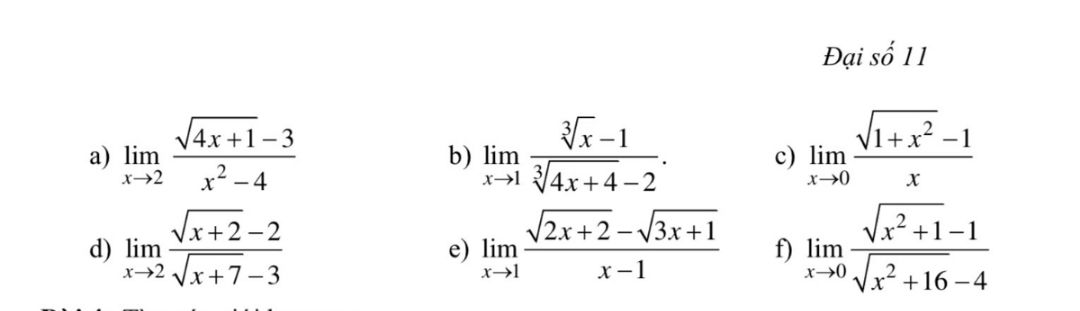 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời



