Giải bài 4 tr 105 sách GK Toán Hình lớp 11
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. Gọi H là chân đường vuông góc hạ từ O tới mặt phẳng (ABC). Chứng minh rằng:
a) H là trực tâm của tam giác ABC;
b) \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\)
Hướng dẫn giải chi tiết
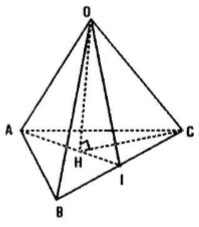
Câu a:
Dễ thấy AH là hình chiếu vuông góc của AO trên mặt phẳng (ABC), vì:
\(\left.\begin{matrix} OA\perp OB\\ OA\perp OC \end{matrix}\right\}\Rightarrow OA\perp (OBC)\)
\(\Rightarrow OA\perp BC'\)
Theo định lý ba đường vuông góc suy ra \(AH\perp BC\)
Tương tự ta cũng có \(CH\perp AB\)
⇒ H là trực tâm của tam giác ABC (đpcm)
Câu b:
Gọi I là giao điểm của AH và BC.
\(\Rightarrow BC\perp AI\)
Mặt khác \(OA\perp BC\) suy ra \(BC\perp (OAI)\Rightarrow BC\perp OI\)
Trong tam giác vuông OAI có đường cao \(OH\Rightarrow \frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OI^2}\)
Trong tam giác vuông OBC có đường cao \(OI\Rightarrow \frac{1}{OI^2}=\frac{1}{OB^2}+\frac{1}{OC^2}\)
Vậy \(\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}.\) (đpcm)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 2 trang 104 SGK Hình học 11
Bài tập 3 trang 104 SGK Hình học 11
Bài tập 5 trang 105 SGK Hình học 11
Bài tập 6 trang 105 SGK Hình học 11
Bài tập 7 trang 105 SGK Hình học 11
Bài tập 8 trang 105 SGK Hình học 11
Bài tập 3.16 trang 145 SBT Hình học 11
Bài tập 3.17 trang 145 SBT Hình học 11
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
-


Qua điểm O cho trước, có bao nhiêu mặt phẳng vuông góc với đường thẳng Δ cho trước?
bởi Mai Hoa
 25/01/2021
25/01/2021
A. 1
B. Vô số
C. 3
D. 2
Theo dõi (0) 1 Trả lời -


Trong không gian cho đường thẳng Δ và điểm O . Qua O có bao nhiêu đường thẳng vuông góc với Δ cho trước?
bởi Nguyễn Thủy Tiên
 26/01/2021
26/01/2021
A. Vô số B. 2 C. 3 D. 1
Theo dõi (0) 1 Trả lời -


A. Mặt phẳng trung trực của đoạn thẳng AB
B. Đường trung trực của đoạn thẳng AB
C. Mặt phẳng vuông góc với AB tại A
D. Đường thẳng qua A và vuông góc với AB
Theo dõi (0) 1 Trả lời -


Khẳng định nào sau đây sai khi nói về đường thẳng vuông góc với mặt phẳng?
bởi Đào Thị Nhàn
 25/01/2021
25/01/2021
A. Nếu đường thẳng d ⊥ (α) thì d vuông góc với hai đường thẳng trong (α)
B. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong (α) thì d ⊥ (α)
C. Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau nằm trong (α) thì d vuông góc với bất kì đường thẳng nào nằm trong (α) .
D. Nếu d ⊥ (α) và đường thẳng a // (α) thì d ⊥ a
Theo dõi (0) 1 Trả lời -
ADMICRO


Mệnh đề nào sau đây có thể sai?
bởi thùy trang
 26/01/2021
26/01/2021
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song.
B. Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song.
C. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song.
D. Một đường thẳng và một mặt phẳng (không chứa đường thẳng đã cho) cùng vuông góc với một đường thẳng thì song song nhau.
Theo dõi (0) 1 Trả lời -


Trong không gian cho đường thẳng Δ và điểm O . Qua O có mấy đường thẳng vuông góc với Δ cho trước?
bởi Bo Bo
 25/01/2021
25/01/2021
A. 1
B. 2
C. 3
D. Vô số.
Theo dõi (0) 1 Trả lời


