Giải bài 3.20 tr 145 SBT Hình học 11
Hai tam giác cân ABC và DBC nằm trong hai mặt phẳng khác nhau có chung cạnh đáy BC tạo nên tứ diện ABCD. Gọi I là trung điểm của cạnh BC.
a) Chứng minh BC ⊥ AD
b) Gọi AH là đường cao của tam giác ADI
Chứng minh rằng AH vuông góc với mặt phẳng (BCD).
Hướng dẫn giải chi tiết
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.18 trang 145 SBT Hình học 11
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
-


Hãy chọn khẳng định đúng?
bởi 이민호
 20/04/2020
20/04/2020
 Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Chứng minh rằng BC vuông góc (SAC)?
bởi N S
 20/04/2020
Giúp em những câu này với ạ !!!
20/04/2020
Giúp em những câu này với ạ !!! Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Chứng minh BC vuông góc (SAB)?
bởi 이민호
 18/04/2020
18/04/2020
Giúp em phần bài tập mẫu:2,4,5 với phần bài tập tự rèn với ạ :((((
 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


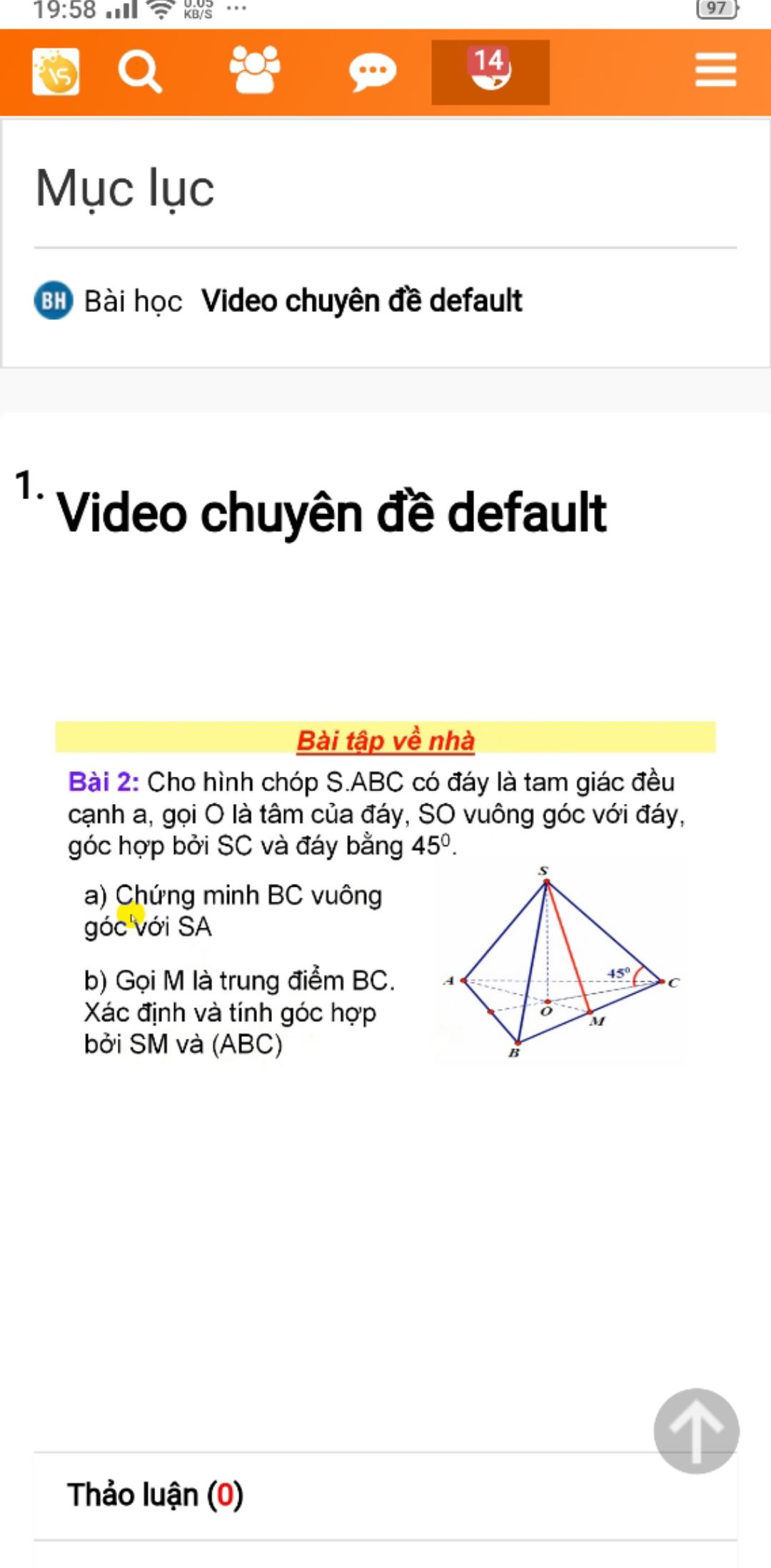
Xác định và tính góc hợp bởi SM và (ABC)?
bởi Khang Pham
 17/04/2020
17/04/2020
Giúp mình câu b với ạ
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -
ADMICRO


Tìm hình chiếu của S trên (ABC)?
bởi Như Quỳnh
 16/04/2020
Giúp em giải bài này với!
16/04/2020
Giúp em giải bài này với! Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời -


Chứng minh BC vuông góc (ABD)?
bởi Như Quỳnh
 16/04/2020
Giúp em giải bài này với ạ.Vẽ hình giúp em luôn nhé. Cảm ơn mn.
16/04/2020
Giúp em giải bài này với ạ.Vẽ hình giúp em luôn nhé. Cảm ơn mn. Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời



