Bài tập 17 trang 103 SGK Hình học 11 NC
Cho hình tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc.
a. Chứng minh tam giác ABC có ba góc nhọn.
b. Chứng minh rằng hình chiếu H của điểm O trên mp(ABC) trùng với trực tâm tam giác ABC.
c. Chứng minh rằng \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Hướng dẫn giải chi tiết
Đặt a = OA, b = OB, c = OC. Ta có:
\(\begin{array}{l}
AB = \sqrt {{a^2} + {b^2}} ,\\
BC = \sqrt {{b^2} + {c^2}} ,\\
AC = \sqrt {{a^2} + {c^2}}
\end{array}\)
Áp dụng định lí cosin trong tam giác ABC ta có :
\(\begin{array}{l}
\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{AB.AC}}\\
= \frac{{{a^2} + {b^2} + {a^2} + {c^2} - {b^2} - {c^2}}}{{AB.AC}}\\
= \frac{{2{a^2}}}{{AB.AC}} > 0
\end{array}\)
⇒ A nhọn. Tương tự B, C là các góc nhọn.
Vậy ΔABC có ba góc nhọn.
b)
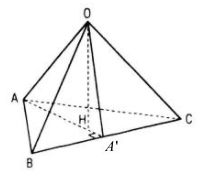
Vì H là hình chiếu của điểm O trên mp(ABC)
nên OH ⊥ (ABC)
Mặt khác OA ⊥ (OBC) nên OA ⊥ BC.
Vậy AH ⊥ BC (định lí ba đường vuông góc), tức
là H thuộc một đường cao của tam giác ABC
Tương tự như trên ta cũng có H thuộc đường cao
thứ hai của tam giác ABC.
Vậy H là trực tâm tam giác ABC
c) Nếu AH ⊥ BC tại A’ thì BC ⊥ OA’.
Vì OH là đường cao của tam giác vuông AOA’ (vuông tại O) và OA’ là đường cao của tam giác vuông BOC (vuông tại O) nên :
\(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{OA{\prime ^2}}},\)
\(\frac{1}{{OA{\prime ^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
Vậy \(\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a; SA⊥(ABCD) và SA=\(\dfrac{a\sqrt{6}}{3}\)
a) chứng minh BD⊥SC
b) Chứng minh BD⊥(SAC)
c) tính góc giữa SC và mặt phẳng (ABCD)
Theo dõi (0) 1 Trả lời -


Bài 3.21 trang 147 sách bài tập Hình học 11
bởi Đào Thị Nhàn
 24/10/2018
Bài 3.21 (Sách bài tập - trang 147)
24/10/2018
Bài 3.21 (Sách bài tập - trang 147)Chứng minh rằng tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó ?
Theo dõi (0) 1 Trả lời -


có bao nhiêu đường thẳng song song với mặt phẳng (alpha) và đi qua điểm O cho trước
Theo dõi (0) 3 Trả lời -
ADMICRO


hình không gian. 11
bởi Tam Thiên
 09/08/2017
09/08/2017
Cho hình chop' SABCD , ABCD là hình vuông cạnh a ,SA vuông góc với (ABCD),SA=2a Tính
a,cos(SB;(ABCD))
b,cos(SC;(SAB))
c,cos(SB,CD)
d,cos ((SBC);(ABCD))
e,cos((SBC);(SAD))
f,cos((SBC);(SCD))
Theo dõi (1) 1 Trả lời -


hình không gian. 11
bởi Tam Thiên
 09/08/2017
09/08/2017
Cho hình lăng trụ đều ABCA'B'C' .AB=a,AA'=3a.Tính :
a,cos(AB;(BCC'B'))
b,cos(AB';CA')
c,cos(AB';(ACC'A'))
d,cos((ABC);(ABC'))
e,cos (AA';(BCA'))
Theo dõi (1) 1 Trả lời



