Bài tập 16 trang 103 SGK Hình học 11 NC
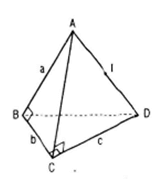
Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc và AB = a, BC = b, CD = c.
a. Tính độ dài AD.
b. Chỉ ra điểm cách đều A, B, C, D
c. Tính góc giữa đường thẳng AD và mặt phẳng (BCD), góc giữa đường thẳng AD và mặt phẳng (ABC).
Hướng dẫn giải chi tiết
a) Ta có: CD ⊥ BC và CD ⊥ AB nên CD ⊥ (ABC)
mà AC ⊂ (ABC) do đó CD ⊥ AC.
Trong tam giác vuông ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} = {a^2} + {b^2}\)
Trong tam giác vuông ACD ta có:
\(\begin{array}{l}
A{D^2} = A{C^2} + C{D^2} = {a^2} + {b^2} + {c^2}\\
\Rightarrow AD = \sqrt {{a^2} + {b^2} + {c^2}}
\end{array}\)
b) Ta có: AB ⊥ BC và AB ⊥ CD suy ra AB ⊥ (BCD) do đó AB ⊥ BD.
Gọi I là trung điểm AD ta có IC = IA = IB = ID.
Vậy I cách đều A, B, C, D.
c) Ta có: AB ⊥ (BCD) ⇒ BD là hình chiếu của ADAD trên (BCD)
Khi đó:
\(\widehat {\left( {AD,\left( {BCD} \right)} \right)} = \widehat {\left( {AD,BD} \right)} = \widehat {ADB}\)
Xét tam giác ABD vuông tại B thì
\(\sin \widehat {ADB} = \frac{{AB}}{{AD}} = \frac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
\( \Rightarrow \widehat {(AD,(BCD))} = arcsin\frac{a}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
Lại có DC ⊥ (ABC) ⇒ AC là hình chiếu của AD trên (ABC)
Khi đó
\(\widehat {\left( {AD,\left( {ABC} \right)} \right)} = \widehat {\left( {AD,AC} \right)} = \widehat {DAC}\)
Xét tam giác ACD vuông tại C thì
\(\sin \widehat {DAC} = \frac{{CD}}{{AD}} = \frac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
\( \Rightarrow \widehat {(AD,(ABC))} = arcsin\frac{c}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-


Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA ⊥ (ABCD) và SA = a√2. Gọi (α) là mặt phẳng qua A và vuông góc với SC, (α) cắt SB, SC, SD lần lượt tại M, N, P.
- Chứng minh AM ⊥ SB, AP ⊥ SD và SM.SB = SN.SC = SP.SD = SA2
- Chứng minh tứ giác AMNP nội tiếp được và có 2 đường chéo vuông góc với nhau.
- Gọi O là giao điểm của AC và BD, K là giao điểm của AN và MP. Chứng minh rằng ba điểm S, K, O thẳng hàng.
- Tính diện tích tứ giác AMNP.
Theo dõi (0) 0 Trả lời -


Chứng minh SH/SB = 2/3 biết hình chóp S.ABCD có đáy là hình vuông cạnh bằng a
bởi Dương Hoàng Lan Anh
 26/01/2020
26/01/2020
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng a, SA ⊥ (ABCD) và SA = a√2. Vẽ đường cao AH của tam giác SAB.
a) Chứng minh: SH/SB = 2/3.
b) Gọi (α) là mặt phẳng qua A và vuông góc với SB, (α) cắt hình chóp S.ABCD theo thiết diện là hình gì ? Tính diện tích của thiết diện.
Theo dõi (0) 1 Trả lời -


Tìm thiết diện của tứ diện S.ABC với mặt phẳng (α) và tính diện tích của thiết diện đó
bởi Dương Hoàng Lan Anh
 26/01/2020
26/01/2020
Cho tứ diện S.ABC có ABC là tam giác đều cạnh a, SA vuông góc với (ABC) và SA = a. Gọi (α) là mặt phẳng đi qua trung điểm M của SC và vuông góc với AB. Tìm thiết diện của tứ diện S.ABC với mặt phẳng (α) và tính diện tích của thiết diện đó.
Theo dõi (0) 0 Trả lời -


Chứng minh CD vuông góc (ABN) biết tứ diện ABCD có tất cả các cạnh bằng nhau
bởi Nguyễn Cầm
 16/01/2020
..
16/01/2020
.. Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Tính xác suất để bạn đố được đúng 100k biết trên cây có 5 lì xì mệnh giá 100k
bởi Thùy Hoàng
 14/01/2020
14/01/2020
 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Tính góc giữa sb và (scd)
bởi Yumi Katana
 02/12/2019
02/12/2019
Cho hình chóp sabcd, đáy abcd là hình chữ nhật, sa vuông với đáy, sa=acan3, ab=a, ad=2a. Tính góc giữa sb và (scd)Theo dõi (0) 5 Trả lời