Bài tập 14 trang 102 SGK Hình học 11 NC
Cho điểm S có hình chiếu trên mp(P) là H. Với điểm M bất kì trên (P) (M không trùng H), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu của đường xiên đó. Chứng minh rằng :
a. Hai đường xiên bằng nhau khi và chỉ khi hai hình chiếu của chúng bằng nhau.
b. Với hai đường xiên cho trước, đường xiên nào dài hơn thì có hình chiếu dài hơn và ngược lại, đường xiên nào có đường chiếu dài hơn thì dài hơn.
Hướng dẫn giải chi tiết
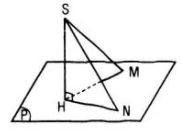
a) Giả sử HM, HN lần lượt là hình chiếu của SM, SN.
* Nếu SM = SN thì ΔSHM = ΔSHN nên HM = HN
Ngược lại nếu HM = HN thì ΔSHM = ΔSHN nên SM = SN
Vậy SM = SN ⇔ HM = HN
b) Áp dụng định lí Pytago, ta có :
\(\begin{array}{l}
S{M^2} - H{M^2} = S{N^2} - H{N^2}( = S{H^2})\\
\Rightarrow S{M^2} - S{N^2} = H{M^2} - H{N^2}
\end{array}\)
Từ đó suy ra : SM > SN ⇔ HM > HN (đpcm)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-
Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, cạnh bên SA vuông góc với đáy. Chứng minh BC vuông góc với (SAB) và BC vuông góc với SB
bởi Nguyễn Thị Loan
31/03/2020
1.Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại B, cạnh bên SA vuông góc với đáy.
a. C/m BC vuông góc với (SAB) và BC vuông góc với SB
b. Gọi H là hình chiếu vuông góc của A trên SB. C/m AH vuông góc với (SBC)
c. Gọi H, K là hình chiếu vuông góc của A trên SB,SC. C/m SC vuông góc với (AHK)
2.Cho hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc với (ABCD)
a. C/m các mặt bên của hình chóp là các tam giác vuông.
b. C/m BD vuông góc với SC
c. Gọi B', D' là hình chiếu của A trên SB, SD . C/m Sc vuông góc với (AB'D')
3. Cho hình chóp S.ABCD, đáy ABD là hình vuông tâm O và các cạnh bên của hình chóp bằng nhau. C/m SO vuông góc với (ABCD)
4. Cho tứ diện đều ABCD (4 mặt là bốn tam giác đều).
a.C/m các cặp cạnh đối diện của tứ diện này vuông góc nhau.
b.C/m đoạn nối trung điểm 2 cạnh đối diện vuông góc với 2 cạnh đó.
Theo dõi (0) 6 Trả lời -
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc (ABCD), SA=a căn 6. Tính góc hợp giữa SC và (SAD).
bởi nhp__
30/03/2020
Mình hỏi câu 17 với ạ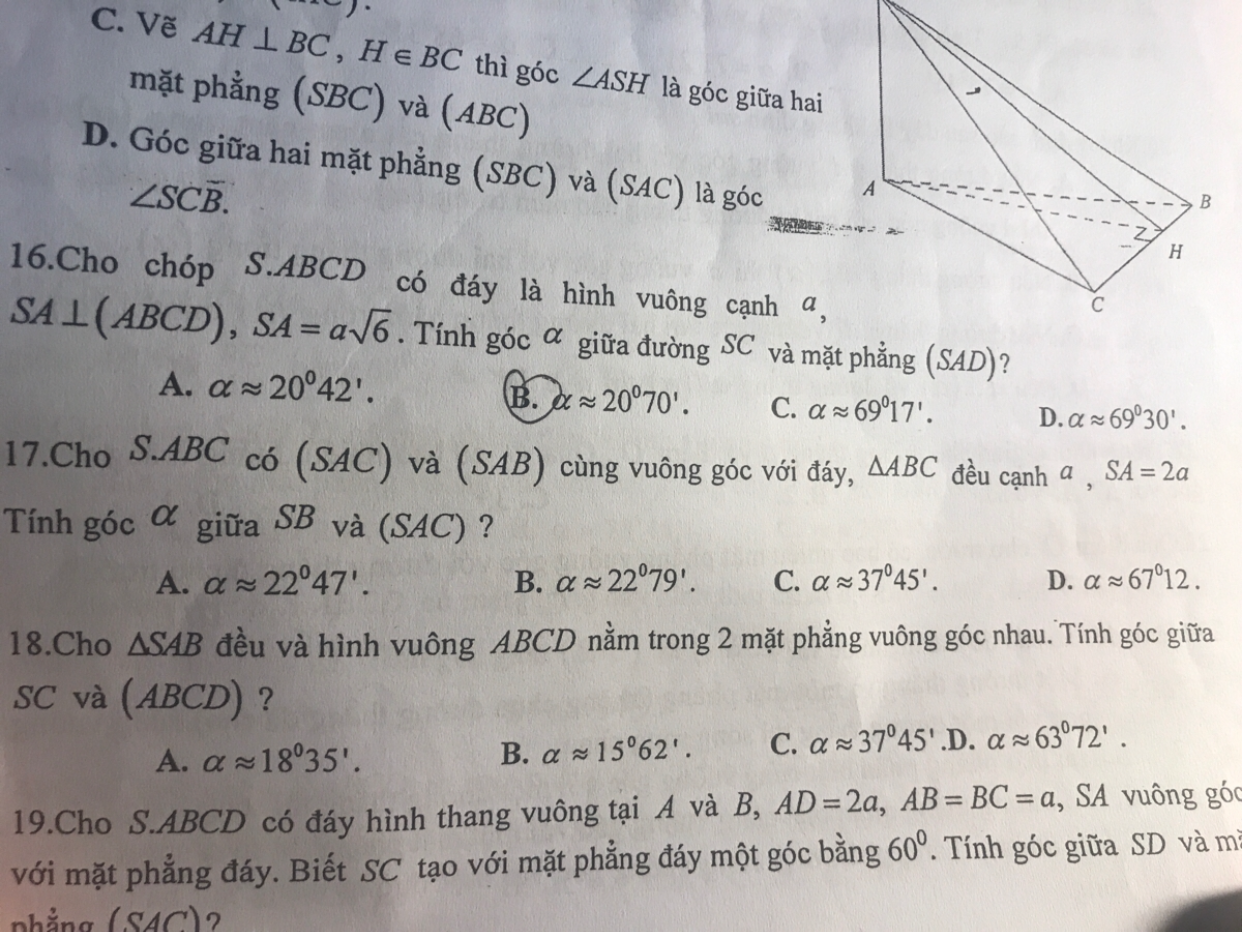
Theo dõi (0) 2 Trả lời -
Cho hình chóp SABCD có SA vuông ( ABCD), SA=2a√3, mặt đáy ABCD là hình chữ nhật tâm O có AB=2a, AD=a. Chứng minh rằng CD uông (SAD).
bởi Uyên Phương
26/03/2020
Cho hinhf chóp SABCD có SA vuông ( ABCD), SA=2a√3, mặt đáy ABCD là hình chữ nhật tâm O có AB=2a, AD=a.
a. Chứng minh rằng Cd vuông (SAD)
b. Tính góc giữa đường SC và (ABCD), góc giấy đường SC và (SAB)
c. Tính góc giữa đường SD và AC
Theo dõi (0) 2 Trả lời -
Cho hình chóp S. ABCD có SC vuông góc với (ABCD), đáy ABCD là hình vuông cạnh bang 1, SC=1. Chứng minh rằng: AB vuông góc (SBC), AD vuông góc (SCD); BD vuông góc (SAC)
bởi PAPWIP
25/03/2020
Góc giữa đt và mp
Theo dõi (0) 1 Trả lời -
ADMICRO
Cho hình chóp S.ABCD có ABCD là hình thoi tâm O. Biết SA=SC; SB=SD. Chứng minh SO vuông góc với (ABCD)
bởi PAPWIP
24/03/2020
Theo dõi (0) 2 Trả lời -
Cho hình chóp S.ABCD có đáy ABC là tam giác cân tại A, SA vuông góc đáy , AH là đường cao trong tam giác ABC. Chứng minh BC vuông góc (SAH)
bởi Quỳnh Như
23/03/2020
Theo dõi (0) 1 Trả lời
