Bài tập 12 trang 102 SGK Hình học 11 NC
Khẳng định “Một đường thẳng vuông góc với hai đường thẳng phân biệt trong mặt phẳng (P) thì nó vuông góc với (P)” có đúng không ? Vì sao ?
Hướng dẫn giải chi tiết
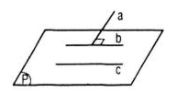
Không đúng vì nếu a ⊥ b và b // c ( trong đó b, c nằm trong (P)) thì a chưa hẳn vuông góc với (P).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 3.21 trang 145 SBT Hình học 11
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
-
Tính độ dài SH theo a?
bởi Anh Quynh
09/04/2020
Theo dõi (0) 0 Trả lời -
Giúp mình làm câu 2,3,4 với ạ
Theo dõi (0) 0 Trả lời -
Khẳng định nào sau đây đúng?
bởi Như Quỳnh
08/04/2020
Giúp mình giải bài này nha.( ghi rõ cách giải giúp mình luôn nha)
Theo dõi (2) 1 Trả lời -
Tính góc giữa cạnh bên SC và mặt đáy ABCD
bởi Nguyễn Thị Loan
07/04/2020
1. Cho hình chóp S.ABCD, đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy và SA = a. Tính góc giữa cạnh bên SC và mặt đáy ABCD.
2. Cho hình chóp tứ giác đều S.ABCD (đáy là hình vuông, chân đường cao của hình chóp trùng tại tâm của đáy) , có cạnh đáy bằng và cạnh bên bằng
. Tính góc giữa cạnh bên và mặt đáy.
3. Tính góc giữa cạnh bên và mặt đáy của tứ diện đều.
Theo dõi (0) 3 Trả lời -
ADMICRO
Chi hình chóp S.ABCD có ABCD là hình vuông cạnh a, SA vuông góc (ABC), SA=2a. Gọi M, N lần lượt là trung điểm cạnh AD và CD. Chứng minh rằng BD vuông góc SC, AN vuông góc BM.
bởi Lee Quỳnh Anh
04/04/2020
I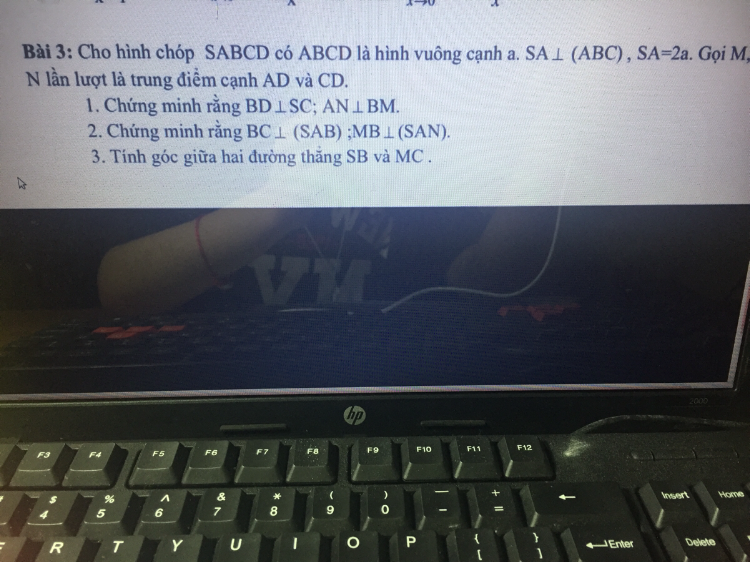
Theo dõi (0) 7 Trả lời -
Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. (gọi là tứ diện vuông; vuông tại O). Gọi H là trực tâm tam giác ABC. Chứng minh OH vuông góc với (ABC)
bởi Nguyễn Thị Loan
04/04/2020
1. Cho tứ diện OABC có ba cạnh OA, OB, OC đôi một vuông góc. (gọi là tứ diện vuông; vuông tại O)
a) Gọi H là trực tâm tam giác ABC. Chứng minh OH vuông góc với (ABC)
b) Gọi H là hình chiếu của O trên mp(ABC) . Chứng minh H là trực tâm tam giác ABC.
Theo dõi (0) 6 Trả lời
