Giải bài 3.21 tr 145 SBT Hình học 11
Chứng minh rằng tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó.
Hướng dẫn giải chi tiết
Phần thuận. Nếu MA = MB = MC nghĩa là M cách đều ba đỉnh của tam giác ABC và MO vuông góc với mặt phẳng (ABC) thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau. Từ đó ta suy ra OA = OB = OC nghĩa là A, B, C nằm trên đường tròn tâm O ngoại tiếp tam giác ABC. Vậy điểm M cách đều ba đỉnh của tam giác ABC thì nằm trên đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn ngoại tiếp tam giác ABC.
Phần đảo. Nếu ta lấy một điểm M bất kì thuộc đường thẳng d nói trên thì ta có ba tam giác vuông MOA, MOB, MOC bằng nhau. Do đó ta suy ra MA = MB = MC nghĩa là điểm M cách đều ba đỉnh của tam giác ABC.
Kết luận. Tập hợp những điểm cách đều ba đỉnh của tam giác ABC là đường thẳng d vuông góc với mặt phẳng (ABC) tại tâm O của đường tròn (C) ngoại tiếp tam giác ABC đó. Người ta thường gọi đường thẳng d là trục của đường tròn (C).
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 3.19 trang 145 SBT Hình học 11
Bài tập 3.20 trang 145 SBT Hình học 11
Bài tập 12 trang 102 SGK Hình học 11 NC
Bài tập 13 trang 102 SGK Hình học 11 NC
Bài tập 14 trang 102 SGK Hình học 11 NC
Bài tập 15 trang 102 SGK Hình học 11 NC
Bài tập 16 trang 103 SGK Hình học 11 NC
Bài tập 17 trang 103 SGK Hình học 11 NC
Bài tập 18 trang 103 SGK Hình học 11 NC
-


Chứng minh AB vuông góc (BD'D)?
bởi Nguyễn Minh Thư
 14/04/2020
14/04/2020
Toán
C6
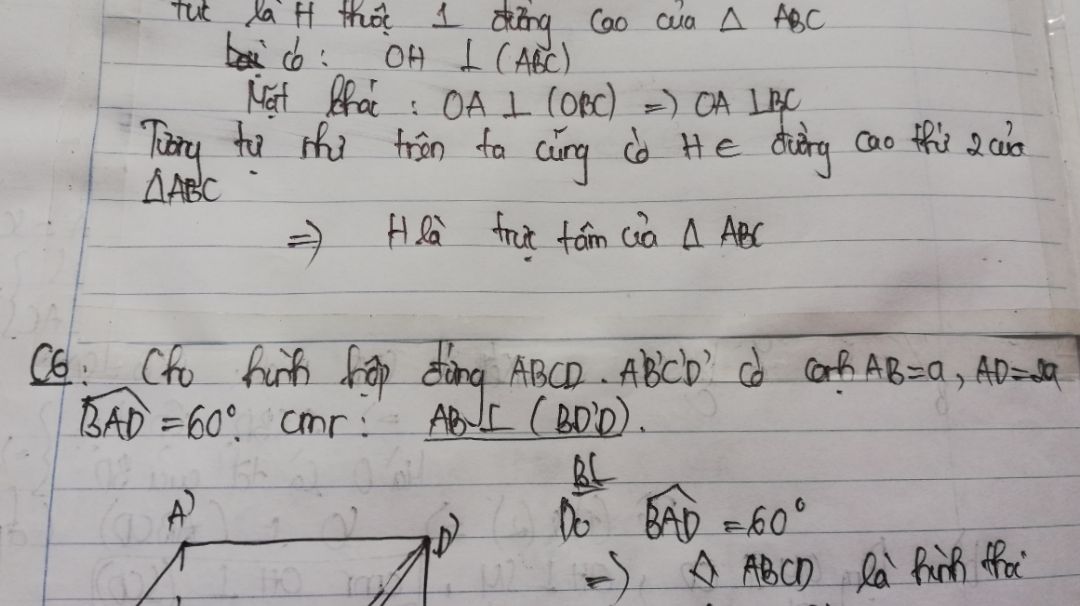 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh EF vuông (SAC) biết hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc (ABCD)
bởi Nguyễn Tâm
 14/04/2020
Hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc (ABCD), AE vuông SB, AF vuông SD. CM: EF vuông (SAC)?!Theo dõi (1) 0 Trả lời
14/04/2020
Hình chóp S.ABCD có đáy ABCD là hình vuông, SA vuông góc (ABCD), AE vuông SB, AF vuông SD. CM: EF vuông (SAC)?!Theo dõi (1) 0 Trả lời -


Chứng minh OH vuông (ABC)?
bởi hltc
 13/04/2020
13/04/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tính góc giữa SC và (SAB)?
bởi Dương PhươngAnh
 13/04/2020
13/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh AM vuông góc (SBC) biết hình chóp S.ABCD có đáy là hình vuông cạnh a
bởi Yến Nhi
 12/04/2020
Cho hình chóp SABCD có đáy là hình vuông cạnh a; SA=2a và vuông góc với đáy. Gọi M, N là hình chiếu của A trên SB, SD. a) Chứng minh: AM 1(SBC); AN 1(SDC). b) Chứng minh: SC 1 (AMN); MN I(SAC) c) Gọi K là giao điểm của SC với mp(AMN). Chứng minh AMKN có hai đường chéo vuông góc. d) Tính góc giữa: SA, SB, SC, SD với đáy. e) Tính góc giữa: SC với (SAB).Theo dõi (0) 0 Trả lời
12/04/2020
Cho hình chóp SABCD có đáy là hình vuông cạnh a; SA=2a và vuông góc với đáy. Gọi M, N là hình chiếu của A trên SB, SD. a) Chứng minh: AM 1(SBC); AN 1(SDC). b) Chứng minh: SC 1 (AMN); MN I(SAC) c) Gọi K là giao điểm của SC với mp(AMN). Chứng minh AMKN có hai đường chéo vuông góc. d) Tính góc giữa: SA, SB, SC, SD với đáy. e) Tính góc giữa: SC với (SAB).Theo dõi (0) 0 Trả lời -


Cho hình chóp SABC có SA vuông góc với đáy là tam giác vuông tại B. Gọi AM là đường cao của tam giác SAB ( M thuộc SB ), khi đó AM không vuông góc với?
bởi Hoàng Thắng
 10/04/2020
Theo dõi (0) 0 Trả lời
10/04/2020
Theo dõi (0) 0 Trả lời





