Giải bài 3 tr 141 sách GK Toán ĐS & GT lớp 11
Cho hàm số \(f(x) =\left\{\begin{matrix} 3x + 2; & x<-1\\ x^{2}-1 & x \geq -1 \end{matrix}\right.\)
a) Vẽ đồ thị của hàm số \(y = f(x)\). Từ đó nêu nhận xét về tính liên tục của hàm số trên tập xác định của nó.
b) Khẳng định nhận xét trên bằng một chứng minh.
Hướng dẫn giải chi tiết bài 3
Câu a:
Vẽ đồ thị hàm số y=f(x).
Tập xác định của hàm số \(\mathbb{R}\)
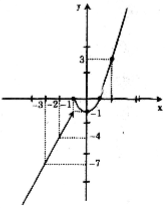
* Đồ thị f(x) = 3x+2 (với x<-1) là phần đường thẳng qua các điểm (-2;-4)(-3;-7).
* Đồ thị f(x) = x2 -1 (với \(x\geq -1\)) là parabol.
* Đỉnh (0;-1)
* Bề lõm hướng lên trên.
* Cắt trục hoành tại (-1;0) và (1;0).
Căn cứ vào đồ thị ta thấy hàm số không liên tục tại điểm x= -1, liên tục trên các khoảng \((-\infty ;-1)\) và \((-1;+\infty )\).
Câu b:
Nếu \(x\geq -1\) thì \(f(x)=x^2-1.\)
Đây là hàm đa thức có tập xác định \([-1;+\infty )\) và hàm số này liên tục trên khoảng \((-1;+\infty )\).
Nếu \(x<-1\) thì \(f(x)=3x+2\)
Đây là hàm đa thức có tập xác định \((-\infty ;-1)\) nên hàm số này liên tục trên khoảng \((-\infty ;-1)\).
Mặt khác \(\lim_{x\rightarrow -1^+}f(x)=0\) và \(\lim_{x\rightarrow -1^-}f(x)=-1\) nên \(\lim_{x\rightarrow -1^+}f(x)\neq \lim_{x\rightarrow -1^-}f(x)\)
Vậy hàm số không liên tục tại x = 1.
-- Mod Toán 11 HỌC247
Video hướng dẫn giải bài 3 SGK
Bài tập SGK khác
Bài tập 1 trang 140 SGK Đại số & Giải tích 11
Bài tập 2 trang 141 SGK Đại số & Giải tích 11
Bài tập 4 trang 141 SGK Đại số & Giải tích 11
Bài tập 5 trang 141 SGK Đại số & Giải tích 11
Bài tập 6 trang 141 SGK Đại số & Giải tích 11
Bài tập 4.32 trang 170 SBT Toán 11
Bài tập 4.33 trang 170 SBT Toán 11
Bài tập 4.34 trang 171 SBT Toán 11
Bài tập 4.35 trang 171 SBT Toán 10
Bài tập 4.36 trang 171 SBT Toán 11
Bài tập 4.37 trang 171 SBT Toán 11
Bài tập 4.38 trang 171 SBT Toán 11
Bài tập 4.39 trang 171 SBT Toán 11
Bài tập 4.40 trang 171 SBT Toán 11
Bài tập 4.41 trang 172 SBT Toán 11
Bài tập 4.42 trang 172 SBT Toán 11
Bài tập 4.43 trang 172 SBT Toán 11
Bài tập 4.44 trang 172 SBT Toán 11
Bài tập 4.45 trang 172 SBT Toán 11
Bài tập 4.46 trang 172 SBT Toán 11
Bài tập 46 trang 172 SGK Toán 11 NC
Bài tập 47 trang 172 SGK Toán 11 NC
Bài tập 48 trang 173 SGK Toán 11 NC
Bài tập 49 trang 173 SGK Toán 11 NC
Bài tập 50 trang 175 SGK Toán 11 NC
Bài tập 51 trang 175 SGK Toán 11 NC
-


Thực hiện chứng minh rằng phương trình: \(\cos 2x = \sin x - 2\) có ít nhất hai nghiệm trong khoảng \(\left( { - {\pi \over 6};\pi } \right)\)
bởi Việt Long
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Thực hiện chứng minh rằng phương trình: \({x^5} - 3x - 7 = 0\) luôn có nghiệm
bởi Tieu Giao
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Tìm giá trị của tham số \(m\) để hàm số sau \(f\left( x \right) = \left\{ \matrix{ {{\sqrt x - 1} \over {{x^2} - 1}},\,\,{\rm{ nếu }}\,\,x \ne 1 \hfill \cr {m^2}{\rm{ ,\,\, nếu }}\,\,x = 1 \hfill \cr} \right.\) liên tục trên \(\left( {0; + \infty } \right)\).
bởi Tay Thu
 25/04/2022
Theo dõi (0) 1 Trả lời
25/04/2022
Theo dõi (0) 1 Trả lời -


Xét tính liên tục của hàm số cho sau trên tập xác định của chúng: \(g\left( x \right) = \left\{ \matrix{ {{1 - x} \over {{{\left( {x - 2} \right)}^2}}},\,\,{\rm{ nếu }}\,\,x \ne 2 \hfill \cr 3{\rm{ ,\,\, nếu }}\,\,x = 2 \hfill \cr} \right.\)
bởi Mai Trang
 26/04/2022
Theo dõi (0) 1 Trả lời
26/04/2022
Theo dõi (0) 1 Trả lời





