Bài tập 47 trang 172 SGK Toán 11 NC
Chứng minh rằng:
a. Hàm số \(f(x)=x^4−x^2+2\) liên tục trên R
b. Hàm số \(f\left( x \right) = \frac{1}{{\sqrt {1 - {x^2}} }}\) liên tục trên khoảng (-1;1) ;
c. Hàm số \(f\left( x \right) = \sqrt {8 - 2{x^2}} \) liên tục trên đoạn [-2;2];
d. Hàm số \(f\left( x \right) = \sqrt {2x - 1} \) liên tục trên nửa khoảng \(\left[ {\frac{1}{2}; + \infty } \right)\)
Hướng dẫn giải chi tiết
a) Hàm số \(f(x)=x^4−x^2+2\) xác định trên R.
Với mọi x0 ∈ R ta có:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^4} - {x^2} + 2} \right)\\
= x_0^4 - x_0^2 + 2 = f\left( {{x_0}} \right)
\end{array}\)
Vậy f liên tục tại x0 nên f liên tục trên R.
b) Hàm số f xác định khi và chỉ khi:
1−x2 > 0 ⇔ −1< x < 1
Vậy hàm số f xác định trên khoảng (-1;1)
Với mọi x0 ∈ (-1 ; 1), ta có:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{\sqrt {1 - {x^2}} }}\\
= \frac{1}{{\sqrt {1 - x_0^2} }} = f\left( {{x_0}} \right)
\end{array}\)
Vậy hàm số f liên tục tại điểm x0. Do đó f liên tục trên khoảng (-1;1)
c) Hàm số \(f\left( x \right) = \sqrt {2x - 1} \) xác định trên đoạn [-2 ; 2]
Với mọi \({x_0} \in \left( { - 2;2} \right)\), ta có:
\(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \sqrt {8 - 2x_0^2} = f\left( {{x_0}} \right)\)
Vậy hàm số f liên tục trên khoảng (- 2;2). Ngoài ra, ta có:
\(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} f\left( x \right) = \sqrt {8 - 2.{{\left( { - 2} \right)}^2}} = 0 = f\left( { - 2} \right)\)
và \(\mathop {\lim }\limits_{x \to {{\left( 2 \right)}^ - }} f\left( x \right) = \sqrt {8 - {{2.2}^2}} = 0 = f\left( 2 \right)\)
Do đó hàm số f liên tục trên đoạn [- 2;2]
d) Hàm số \(f\left( x \right) = \sqrt {2x - 1} \) xác định trên nửa khoảng \(\left[ {\frac{1}{2}; + \infty } \right)\)
Với \({x_0} \in \left( {\frac{1}{2}; + \infty } \right)\) ta có:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \sqrt {2x - 1} \\
= \sqrt {2{x_0} - 1} = f\left( {{x_0}} \right)
\end{array}\)
Nên hàm số liên tục trên khoảng \(\left( {\frac{1}{2}; + \infty } \right)\)
Mặt khác ta có:
\(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} \sqrt {2x - 1} = 0 = f\left( {\frac{1}{2}} \right)\)
Do đó hàm số f liên tục trên nửa khoảng \(\left[ {\frac{1}{2}; + \infty } \right)\)
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-

 11
11 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tìm m để hàm số f(x)=(x^2-x-2)/(x-2) khi x ≠ 2 và f(x)=m khi x=2 liên tục tại x=2?
bởi Quỳnh Huỳnh
 24/03/2020
24/03/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


Tính giới hạn day số (2n-1)(n-1)(3n-4)/(6n+1)^3
bởi Huan Nguyen
 23/03/2020
Mn giúp e vs ạ
23/03/2020
Mn giúp e vs ạ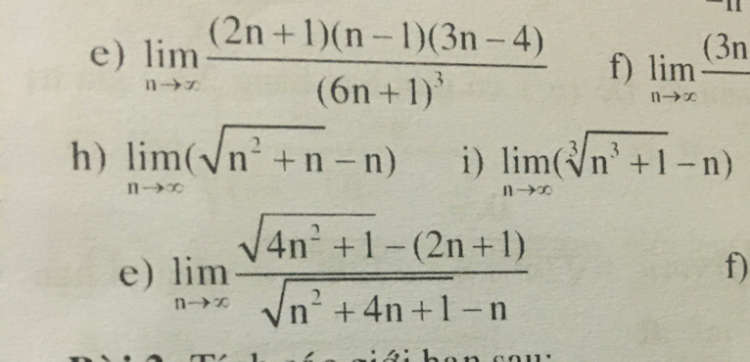 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Xét tính liên tục của hàm số trên R biết f(x)=(x^2-3x+2)/|x-1| khi x khác 1, f(x)=a khi x=1.
bởi Quy Nguyễn Trọng Từ
 23/03/2020
Giúp mình với!
23/03/2020
Giúp mình với!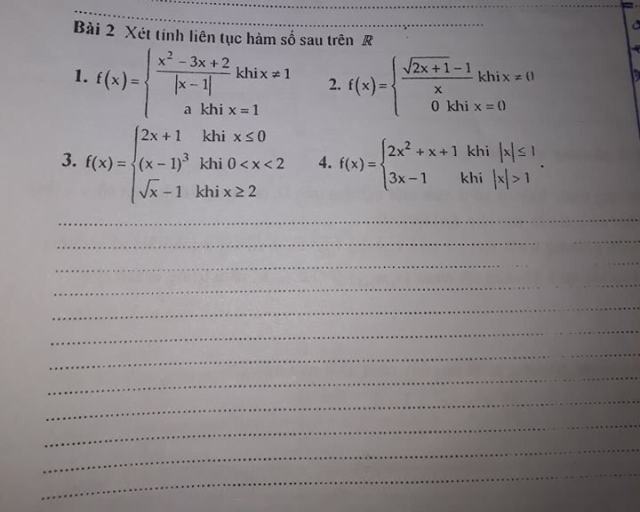 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





