Bài tập 46 trang 172 SGK Toán 11 NC
Chứng minh rằng:
a. Các hàm số \(f(x)=x^3−x+3\) và \(g\left( x \right) = \frac{{{x^3} - 1}}{{{x^2} + 1}}\) liên tục tại mọi điểm x ∈ R.
b. Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{{x^2} - 3x + 2}}{{x - 2}},\,\,\,x \ne 2\\
1,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 2
\end{array} \right.\) liên tục tại điểm x = 2
c. Hàm số \(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{{x^3} - 1}}{{x - 1}},\,\,\,x \ne 1\\
2,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 1
\end{array} \right.\) gián đoạn tại điểm x = 1
Hướng dẫn giải chi tiết
a) Hàm số \(f(x)=x^3−x+3\) xác định trên R.
Với mọi x0 ∈ R, ta có:
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^3} - x + 3} \right)\\
= x_0^3 - {x_0} + 3 = f\left( {{x_0}} \right)
\end{array}\)
Vậy f liên tục tại điểm x0. Do đó hàm số f liên tục trên R.
Hàm số g là hàm phân thức nên g liên tục trên tập xác định D = R.
b) Với mọi x ≠ 2, ta có:
\(\begin{array}{l}
f\left( x \right) = \frac{{{x^2} - 3x + 2}}{{x - 2}}\\
= \frac{{\left( {x - 1} \right)\left( {x - 2} \right)}}{{x - 2}} = x - 1
\end{array}\)
Do đó \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = \mathop {\lim }\limits_{x \to 2} \left( {x - 1} \right) = 1 = f\left( 2 \right)\)
Vậy hàm số f liên tục tại điểm x = 2
c) Với mọi x ≠ 1, ta có:
\(f\left( x \right) = \frac{{{x^3} - 1}}{{x - 1}} = {x^2} + x + 1\)
Do đó \(\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + x + 1} \right) = 3 \ne 2 = f\left( 1 \right)\)
Vậy hàm số f gián đoạn tại điểm x = 1.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
-


Bài tập hàm số liên tục
bởi Nguyenthiquy
 04/04/2020
Mọi người giải giúp mình với ạ
04/04/2020
Mọi người giải giúp mình với ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho hàm số f(x) xác định và liên tục trên [-3,3] với f(x)=căn x 3 - căn x-3 / x với x khác 0. Tính f(0)
bởi Thảo Nhyy
 04/04/2020
Cho hàm số f(x) xác định và liên tục trên [-3,3] với f(x)=căn x 3 - căn x-3 / x với x khác 0 . Tính f(0)
04/04/2020
Cho hàm số f(x) xác định và liên tục trên [-3,3] với f(x)=căn x 3 - căn x-3 / x với x khác 0 . Tính f(0) Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Tính lim f(x)=[(x-5)/{(căn 2*x-1)-3}]
bởi Bùi Thị Cẩm Ly
 31/03/2020
31/03/2020
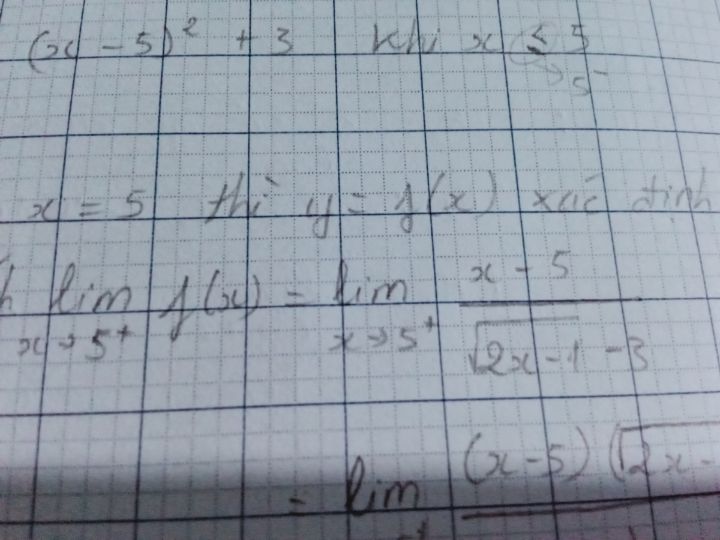 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm tất cả các giấ trị thực của m để phương trình m(x^2019-1)(x-2)^2020+2x-3=0 vô nghiệm.
bởi Thanh Vũ Phương
 29/03/2020
Giúp mình câu 43, 44 nha
29/03/2020
Giúp mình câu 43, 44 nha Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời





