Giải bài 4.35 tr 171 SBT Toán 11
Cho hàm số xác định trên khoảng chứa điểm
Chứng minh rằng nếu \(\mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = L\) thì hàm số liên tục tại điểm .
Hướng dẫn giải chi tiết
Đặt \(g\left( x \right) = \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} - L\)
Ta có xác định trên và \(\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = 0\)
Mặt khác, \(f\left( x \right) = f\left( {{x_0}} \right) + L.\left( {x - {x_0}} \right) + \left( {x - {x_0}} \right)g\left( x \right)\) nên
\(\begin{array}{l}
\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( {{x_0}} \right) + L\left( {x - {x_0}} \right) + \left( {x - {x_0}} \right)g\left( x \right)} \right]\\
= \mathop {\lim }\limits_{x \to {x_0}} f\left( {{x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} L\left( {x - {x_0}} \right) + \mathop {\lim }\limits_{x \to {x_0}} \left( {x - {x_0}} \right).\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = f\left( {{x_0}} \right)
\end{array}\)
Vậy hàm số liên tục tại
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 4.33 trang 170 SBT Toán 11
Bài tập 4.34 trang 171 SBT Toán 11
Bài tập 4.36 trang 171 SBT Toán 11
Bài tập 4.37 trang 171 SBT Toán 11
Bài tập 4.38 trang 171 SBT Toán 11
Bài tập 4.39 trang 171 SBT Toán 11
Bài tập 4.40 trang 171 SBT Toán 11
Bài tập 4.41 trang 172 SBT Toán 11
Bài tập 4.42 trang 172 SBT Toán 11
Bài tập 4.43 trang 172 SBT Toán 11
Bài tập 4.44 trang 172 SBT Toán 11
Bài tập 4.45 trang 172 SBT Toán 11
Bài tập 4.46 trang 172 SBT Toán 11
Bài tập 46 trang 172 SGK Toán 11 NC
Bài tập 47 trang 172 SGK Toán 11 NC
Bài tập 48 trang 173 SGK Toán 11 NC
Bài tập 49 trang 173 SGK Toán 11 NC
Bài tập 50 trang 175 SGK Toán 11 NC
Bài tập 51 trang 175 SGK Toán 11 NC
-


Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c) thì nó liên tục trên (a; c).
bởi Bùi Anh Tuấn
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Cho ví dụ về một hàm số liên tục trên (a; b] và trên (b; c) nhưng không liên tục trên (a; c).
bởi thi trang
 01/03/2021
Theo dõi (0) 1 Trả lời
01/03/2021
Theo dõi (0) 1 Trả lời -


Tính giới hạn của hàm số
bởi Nguyễn Thị Hồng Nhung
 24/02/2021
Giúp mình với ạ
24/02/2021
Giúp mình với ạ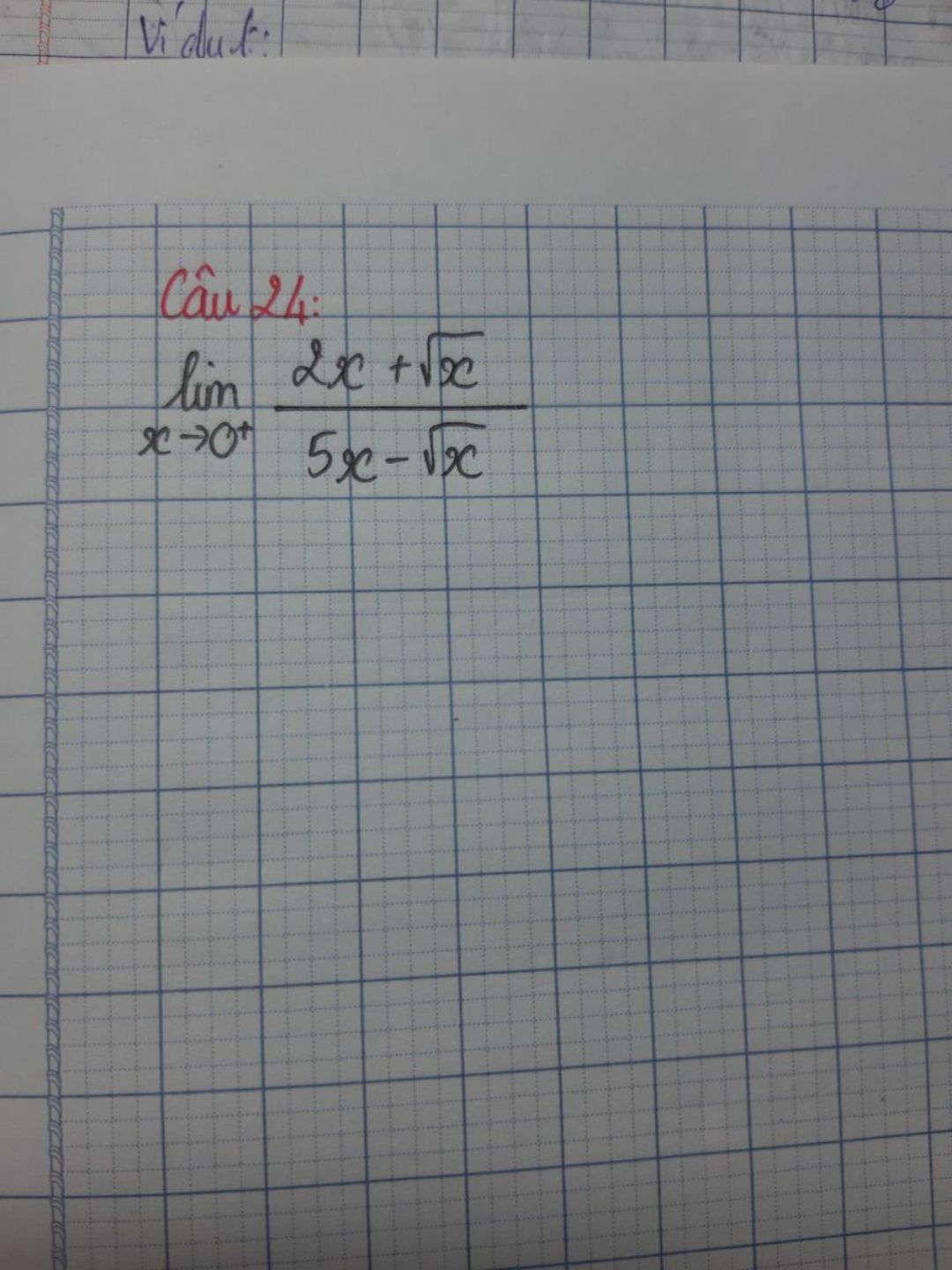 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời





