Giải bài 4.37 tr 171 SBT Toán 11
Xét tính liên tục của các hàm số sau trên tập xác định của chúng:
a) \(f\left( x \right) = \left\{ \begin{array}{l}
\frac{{{x^2} - 2}}{{x - \sqrt 2 }},\,\,x \ne \sqrt 2 \\
2\sqrt 2 ,\,\,\,\,\,\,\,\,x = \sqrt 2
\end{array} \right.\)
b) \(g\left( x \right) = \left\{ \begin{array}{l}
\frac{{1 - x}}{{{{\left( {x - 2} \right)}^2}}},\,\,x \ne 2\\
3,\,\,\,\,\,\,\,\,x = 2
\end{array} \right.\)
Hướng dẫn giải chi tiết
a) TXĐ:
Nếu \(x \ne \sqrt 2\) thì \(f\left( x \right) = \frac{{{x^2} - 2}}{{x - \sqrt 2 }}\)
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng \(\left( { - \infty ;\sqrt 2 } \right)\) và \(\left( {\sqrt 2 ; + \infty } \right)\)
Với \(x = \sqrt 2 \), ta có:
\(f\left( {\sqrt 2 } \right) = 2\sqrt 2 \)
\(\mathop {\lim }\limits_{x \to \sqrt 2 } f\left( x \right) = \mathop {\lim }\limits_{x \to \sqrt 2 } \frac{{{x^2} - 2}}{{x - \sqrt 2 }} = \mathop {\lim }\limits_{x \to \sqrt 2 } \left( {x + \sqrt 2 } \right) = 2\sqrt 2 \)
Vậy hàm số liên tục tại \(x = \sqrt 2 \)
Kết luận: Hàm số liên tục trên
b) TXĐ:
Với thì \(g\left( x \right) = \frac{{1 - x}}{{{{\left( {x - 2} \right)}^2}}}\)
Đây là hàm phân thức hữu tỉ nên liên tục trên các khoảng và
Với , ta có:
\(\mathop {\lim }\limits_{x \to 2} \frac{{1 - x}}{{{{\left( {x - 2} \right)}^2}}} = - \infty \ne f\left( 2 \right)\)
Hàm số gián đoạn tại
Vậy hàm số liên tục trên các khoảng và nhưng gián đoạn tại .
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Bài tập 4.35 trang 171 SBT Toán 10
Bài tập 4.36 trang 171 SBT Toán 11
Bài tập 4.38 trang 171 SBT Toán 11
Bài tập 4.39 trang 171 SBT Toán 11
Bài tập 4.40 trang 171 SBT Toán 11
Bài tập 4.41 trang 172 SBT Toán 11
Bài tập 4.42 trang 172 SBT Toán 11
Bài tập 4.43 trang 172 SBT Toán 11
Bài tập 4.44 trang 172 SBT Toán 11
Bài tập 4.45 trang 172 SBT Toán 11
Bài tập 4.46 trang 172 SBT Toán 11
Bài tập 46 trang 172 SGK Toán 11 NC
Bài tập 47 trang 172 SGK Toán 11 NC
Bài tập 48 trang 173 SGK Toán 11 NC
Bài tập 49 trang 173 SGK Toán 11 NC
Bài tập 50 trang 175 SGK Toán 11 NC
Bài tập 51 trang 175 SGK Toán 11 NC
-


Dùng định nghĩa xét tính liên tục của hàm số \(f(x) = x^3+ 2x - 1\) tại \(x_0= 3\).
bởi Nguyễn Thanh Thảo
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời -


Hãy tìm hai số a và b thỏa mãn 1 < a < b < 2, sao cho phương trình trong Ví dụ 3 ở trên có ít nhất một nghiệm thuộc khoảng (a; b).
bởi Nguyen Dat
 23/02/2021
Theo dõi (0) 1 Trả lời
23/02/2021
Theo dõi (0) 1 Trả lời -


Trong biểu thức xác định h(x) cho ở Ví dụ 2, cần thay số 5 bởi số nào để được một hàm số mới liên tục trên tập số thực R?
bởi Bao Chau
 24/02/2021
Theo dõi (0) 1 Trả lời
24/02/2021
Theo dõi (0) 1 Trả lời -


Hàm số nào sau đây không liên tục tại x=0?
bởi Kim Thoa
 24/06/2020
Chỉ mình cách tính 2 câu này với
24/06/2020
Chỉ mình cách tính 2 câu này với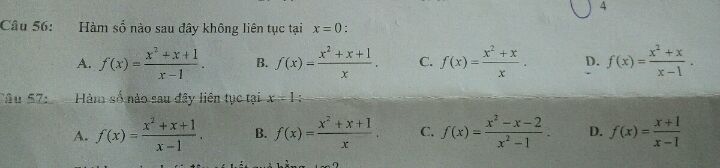 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời





