Toán 11 Cánh Diều Bài 3: Hàm số lượng giác và đồ thị

Lý thuyết10 Trắc nghiệm48 BT SGK 0 FAQ

Nội dung bài Hàm số lượng giác và đồ thị Toán 11 Cánh Diều sẽ giới thiệu đến các em khái niệm, tính chất của các Hàm số lượng giác và tìm hiểu về Đồ thị của các hàm số lượng giác. Thông qua các ví dụ minh họa có hướng dẫn giải các em sẽ nắm vững được nội dung phần này và vận dụng vào các bài tập tương tự. Chúc các em học thật tốt!

QUẢNG CÁO

1. Tóm tắt lý thuyết

1.1. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a. Hàm số chẵn, hàm số lẻ

b. Hàm số tuần hoàn

1.2. Hàm số \(y = \sin x\)

a. Định nghĩa

b. Đồ thị của hàm số \(y = \sin x\)

c. Tính chất của hàm số \(y = \sin x\)

1.3. Hàm số \(y = \cos x\)

a. Định nghĩa

b. Đồ thị của hàm số \(y = \cos x\)

c. Tính chất của hàm số \(y = \cos x\)

1.4. Hàm số \(y = \tan x\)

a. Định nghĩa

b. Đồ thị của hàm số \(y = \tan x\)

c. Tính chất của hàm số \(y = \tan x\)

1.5. Hàm số \(y = \cot x\)

a. Định nghĩa

b. Đồ thị của hàm số \(y = \cot x\)

c. Tính chất của hàm số \(y = \cot x\)

2. Bài tập minh hoạ

3. Luyện tập Bài 3 Chương 1 Toán 11 Cánh Diều

3.1. Trắc nghiệm

3.2. Bài tập SGK

4. Hỏi đáp Bài 3 Chương 1 Toán 11 Cánh Diều

Tóm tắt lý thuyết

1.1. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a. Hàm số chẵn, hàm số lẻ

Cho hàm số \(y = f(x)\) với tập xác định D.

Hàm số \(y = f(x)\) được gọi là hàm số chẵn nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = f(x)\).

Hàm số \(y = f(x)\) được gọi là hàm số lẻ nếu \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = f(x)\).

- Chú ý:

Đồ thị hàm số chẵn nhận trục tung làm trục đối xứng.

Đồ thị hàm số lẻ nhận góc toạ độ làm tâm đối xứng.

b. Hàm số tuần hoàn

Cho hàm số \(y = f(x)\) với tập xác định D. Hàm số \(y = f(x)\) được gọi là tuần hoàn nếu tồn tại một số T khác 0 sao cho \(\forall x \in D\), ta có:

\(x + T \in D\) và \(x - T \in D\).
\(f(x+T) = f(x)\).

Số T dương nhỏ nhất thoả mãn (nếu có) các tính chất trên được gọi là chu kì của hàm số tuần hoàn đó.

- Nhận xét:

Cho hàm số tuần hoàn chu kì T. Từ đồ thị hàm số đó trên đoạn [a; a+T], ta dịch chuyển song song với trục hoành sang phải (hoặc sang trái) theo đoạn có độ dài T thì được đồ thị hàm số trên đoạn [a+T; a+2T] (hoặc [a-T; a]).

1.2. Hàm số \(y = \sin x\)

a. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực sinx được gọi là hàm số

\(y = \sin x\). Tập xác định của hàm số \(y = \sin x\) là \(ℝ\).

b. Đồ thị của hàm số \(y = \sin x\)

- Đồ thị hàm số \(y = \sin x\) trên \(ℝ\) được biểu diễn như sau:

c. Tính chất của hàm số y = sinx

Hàm số \(y = \sin x\) là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.

Hàm số\(y = \sin x\) tuần hoàn chu kì \(2\pi \).

Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( {\frac{{ - \pi }}{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{{ \pi }}{2} + k2\pi ;\frac{3pi }{2} + k2\pi } \right)\) với \(k \in ℤ\).

- Nhận xét: Dựa vào đồ thị của hàm số \(y = \sin x\), ta thấy \(\sin x = 0\) tại những giá trị \(x = k\pi (k \in ℤ\). Vì vậy, tập hợp các số thực x sao cho \(\sin x \ne 0\) là \(E{\rm{ }} =ℝ \backslash \{ k\pi |k \in ℤ\} \).

1.3. Hàm số \(y = \cos x\)

a. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực cosx được gọi là hàm số

\(y = \cos x\). Tập xác định của hàm số \(y = \cos x\) là ℝ.

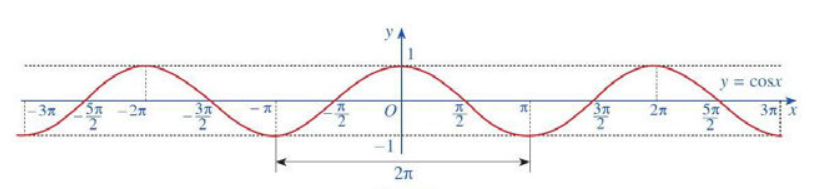
b. Đồ thị của hàm số \(y = \cos x\)

c. Tính chất của hàm số \(y = \cos x\)

Hàm số \(y = \cos x\) là hàm số chẵn, có đồ thị đối xứng qua trục tung.

Hàm số \(y = \cos x\) tuần hoàn chu kì \(2\pi \).

Hàm số \(y = \cos x\) đồng biến trên mỗi khoảng \(( - \pi + k2\pi ;k2\pi )\), nghịch biến trên mỗi khoảng \((k2\pi ;\pi + k2\pi )\) với \(k \in \)ℤ.

- Nhận xét: Dựa vào đồ thị của hàm số \(y = \cos x\), ta thấy cosx = 0 tại những giá trị \(x = \frac{\pi }{2} + k\pi (k \in ℤ\). Vì vậy, tập hợp các số thực x sao cho \(\cos x \ne 0\) là \(D = ℝ\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in ℤ} \right\}\).

1.4. Hàm số \(y = \tan x\)

a. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực tanx được gọi là hàm số

\(y = \tan x\). Tập xác định của hàm số \(y = \tan x\) là \(D = R\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in Z} \right\}\).

b. Đồ thị của hàm số \(y = \tan x\)

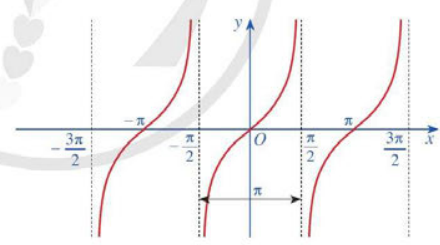
c. Tính chất của hàm số \(y = \tan x\)

Hàm số \(y = \tan x\) là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.

Hàm số \(y = \tan x\) tuần hoàn chu kì .

Hàm số \(y = \tan x\) đồng biến trên mỗi khoảng \(\left( {\frac{{ - \pi }}{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với \(k \in \)ℤ.

1.5. Hàm số \(y = \cot x\)

a. Định nghĩa

Quy tắc đặt tương ứng mỗi số thực x với một số thực cotx được gọi là hàm số

\(y = \cot x\). Tập xác định của hàm số \(y = \cot x\) là \(E = R\backslash \left\{ {k\pi |k \in Z} \right\}\).

b. Đồ thị của hàm số \(y = \cot x\)

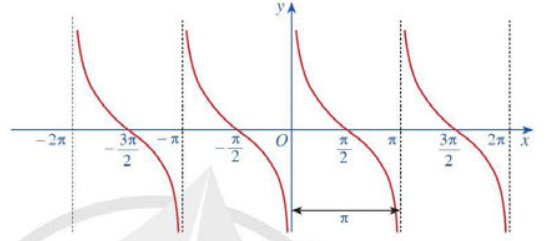
c. Tính chất của hàm số \(y = \cot x\)

Hàm số \(y = \cot x\) là hàm số lẻ, có đồ thị đối xứng qua gốc tọa độ O.

Hàm số \(y = \cot x\) tuần hoàn chu kì π.

Hàm số \(y = \cot x\) nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right)\), với \(k \in \)ℤ.

ADMICRO

3. Luyện tập Bài 3 Chương 1 Toán 11 Cánh Diều

Học xong bài này, các em có thể:

- Nhận biết các khái niệm về hàm số chẵn, hàm số lẻ, hàm số tuần hoàn, các đặc trưng hình học của đồ thị hàm số chẵn, hàm số lẻ, hàm số tuần hoàn, các hàm số lượng giác y = sin x, y = cos x, y = tan x, y = cot x thông qua đường tròn lượng giác.

- Mô tả bảng giá trị của bốn hàm số lượng giác đó trên một chu kì. Vẽ được đồ thị các hàm số y = sin x, y = cos x, y = tan x, y = cot x.

- Giải thích được: tập xác định, tập giá trị, tính chất chẵn, lẽ; tính tuần hoàn; chu kì; khoảng đồng biến, nghịch biến của các hàm số y = sin x, y = cos x, y = tan x, y = cot x dựa vào đồ thị.

- Giải quyết được một số vấn đề thực tiễn gắn với hàm số lượng giác (ví dụ: một bài toán có liên quan đến dao động điều hòa trong Vật lí,...).

3.1. Trắc nghiệm Bài 3 Chương 1 Toán 11 Cánh Diều

Để cũng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Toán 11 Cánh Diều Chương 1 Bài 3 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Hàm số nào là hàm số chẵn trong các hàm số sau?
- A. \(y=\sin x\)
- B. \(y=\cos x\)
- C. \(y=\tan x\)
- D. \(y=\cot \)
Câu 2:
Hàm số nào có đồ thị đối xứng qua trục tung trong các hàm số sau?
- A. \(y=\sin \,x\cos 2x\)
- B. \(y={{\sin }^{3}}x.\cos \left( x-\frac{\pi }{2} \right)\)
- C. \(y=\frac{\tan \,x}{{{\tan }^{2}}x+1}\)
- D. \(y=\cos x{{\sin }^{3}}x\)
Câu 3:
Hàm số nào là hàm số lẻ trong các hàm số sau?
- A. \(y=\sin \left( \frac{\pi }{2}-x \right)\)
- B. \(y={{\sin }^{2}}\)
- C. \(y=\frac{\cot x}{\cos x}\)
- D. \(y=\frac{\tan x}{\sin x}\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2 Bài tập SGK Bài 3 Chương 1 Toán 11 Cánh Diều

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 1 Bài 3 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Toán 11 Cánh Diều

Khởi động trang 22 SGK Toán 11 Cánh Diều Tập 1 - CD

Hoạt động 1 trang 22 SGK Toán 11 Cánh Diều tập 1 - CD

Luyện tập 1 trang 23 SGK Toán 11 Cánh Diều tập 1 - CD

Hoạt động 2 trang 23 SGK Toán 11 Cánh Diều tập 1 - CD

Luyện tập 2 trang 23 SGK Toán 11 Cánh Diều tập 1 - CD

Hoạt động 3 trang 24 SGK Toán 11 Cánh Diều tập 1 - CD

Hoạt động 4 trang 24 SGK Toán 11 Cánh Diều tập 1 - CD

Hoạt động 5 trang 25 SGK Toán 11 Cánh Diều tập 1 -CD

Hoạt động 6 trang 26 SGK Toán 11 Cánh Diều tập 1 - CD

Hoạt động 7 trang 26 SGK Toán 11 Cánh Diều tập 1 - CD

Hoạt động 8 trang 27 SGK Toán 11 Cánh Diều tập 1 - CD

Luyện tập 3 trang 25 SGK Toán 11 Cánh Diều tập 1 - CD