Toán 11 Cánh Diều Bài tập cuối Chương 1

a. Công thức cộng

\(\begin{array}{l}
\sin (a + b) = \sin a\cos b + \cos a\sin b\\
\sin (a - b) = \sin a\cos b - \cos a\sin b\\
\cos (a + b) = \cos a\cos b - \sin a\sin b\\
\cos (a - b) = \cos a\cos b + \sin a\sin b\\
\tan (a + b) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\
\tan (a - b) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}
\end{array}\)

b. Công thức nhân đôi

\(\begin{array}{l}
\sin 2a = 2\sin a\cos a\\
\cos 2a = {\cos ^2}a - {\sin ^2}a\\
\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}
\end{array}\)

c. Công thức biến đổi tích thành tổng

\(\begin{array}{l}
\cos a\cos b = \frac{1}{2}[\cos (a + b) + \cos (a - b)]\\
\sin a\sin b = \frac{{ - 1}}{2}[\cos (a + b) - \cos (a - b)]\\
\sin a\cos b = \frac{1}{2}[\sin (a + b) + \sin (a - b)]
\end{array}\)

d. Công thức biến đổi tổng thành tích

\(\begin{array}{l}
\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\\
\cos u - \cos v =  - 2\sin \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\\
\sin u + \sin v = 2\sin \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\\
\sin u - \sin v = 2\cos \frac{{u + v}}{2}\sin \frac{{u - v}}{2}
\end{array}\)

e. Công thức hạ bậc

\(\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\).

\({\cos ^2}a = \frac{{1 + \cos 2a}}{2};{\sin ^2}a = \frac{{1 - \cos 2a}}{2}\)

a. Hai góc đối nhau (\(\alpha \) và -\(\alpha \) )

\(\sin (-\alpha )=-\sin (\alpha )\)

\(\cos ( - \alpha ) =  \cos (\alpha )\)

\(\tan ( - \alpha ) =  - \tan (\alpha )\)

\(\cot ( - \alpha ) =  - \cot (\alpha )\)

b. Hai góc hơn kém nhau (\(\alpha \) và \(\alpha +\pi \))

\(\sin (\alpha +\pi )=-\sin (\alpha )\)

\(\cos (\alpha  + \pi ) =  - \sin (\alpha )\)

\(\tan (\alpha  + \pi ) =  \tan (\alpha )\)

\(\cot (\alpha  + \pi ) =  \cot (\alpha )\)

c. Hai góc bù nhau (\(\alpha \) và \(\pi -\alpha \))

\(\sin (\pi -\alpha )=\sin (\alpha )\)

\(\cos (\pi -\alpha )=-\cos (\alpha )\)

\(\tan (\pi -\alpha )=-\tan (\alpha )\)

\(\cot (\pi -\alpha )=-\cot \alpha \)

d. Hai góc phụ nhau (\(\alpha \) và \(\frac{\pi }{2}-\alpha \))

\(\sin \left( \frac{\pi }{2}-\alpha  \right)=\cos \alpha \)

\(\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \)

\(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \)

\(\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \)

a. Hàm số sinx = m

- TXĐ : D = R và \( - 1 \le \sin x \le 1,\forall x \in R\).

- Là hàm số lẻ.

- Hàm số đồng biến trên \(\left( {\frac{{ - \pi }}{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\).

- Hàm số nghịch biến trên \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).

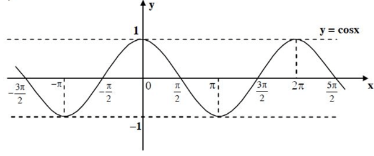
b. Hàm số cosx = m

- TXĐ : D = R và \( - 1 \le \cos x \le 1,\forall x \in R\).

- Là hàm số chẵn.

- Là hàm số có tuần hoàn chu kì π.

- Hàm số đồng biến trên \(\left( { - \pi  + k2\pi ;k2\pi } \right)\).

- Hàm số nghịch biến trên \(\left( {k2\pi ;\pi  + k2\pi } \right)\).

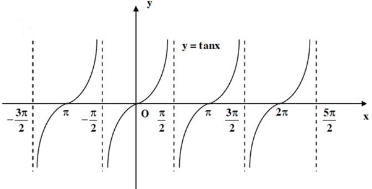
c. Hàm số tanx = m

- TXĐ : D = R.

- Là hàm số lẻ

- Là hàm số có tuần hoàn chu kì π.

- Hàm số đồng biến trên \(\left( {\frac{{ - \pi }}{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).

- Có các đường tiệm cận \(x = \frac{\pi }{2} + k\pi \).

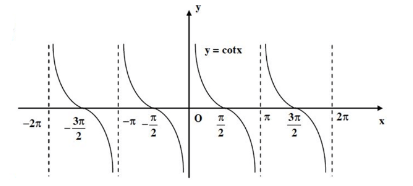
d. Hàm số cotx = m

- TXĐ : D = R \ \(\left\{ {k\pi , \in Z} \right\}\).

- Là hàm số lẻ

- Là hàm số có tuần hoàn chu kì π.

- Hàm số nghịch biến trên \(\left( {k\pi ;\pi  + k\pi } \right)\).

- Có các đường tiệm cận \(x = k\pi \).

- Đặc biệt

Ví dụ

Giải các phương trình lượng giác sau:

a. \({\sin ^4}x + {\cos ^4}\left( {x + \frac{\pi }{4}} \right) = \frac{1}{4}\)

b. \({\sin ^4}x + {\cos ^4}x = 2\sin x\cos x - \frac{1}{2}{\cos ^2}2x\)

c. \(\tan x + \frac{{\cos x}}{{1 + \sin x}} = 1\)

d. \(\cot x = \tan x + \frac{{2\cos 4x}}{{\sin 2x}}\)

Lời giải:

a. \({\sin ^4}x + {\cos ^4}\left( {x + \frac{\pi }{4}} \right) = \frac{1}{4}\)

\( \Leftrightarrow \frac{{{{(1 - \cos 2x)}^2}}}{4} + \frac{{{{\left[ {1 + \cos (2x + \frac{\pi }{2})} \right]}^2}}}{4} = \frac{1}{4}\)\( \Leftrightarrow {(1 - \cos 2x)^2} + {(1 - \sin 2x)^2} = 1\)

\( \Leftrightarrow \cos 2x + \sin 2x = 1 \Leftrightarrow \cos \left( {2x - \frac{\pi }{4}} \right) = \frac{{\sqrt 2 }}{2} \Leftrightarrow \left[ \begin{array}{l}2x - \frac{\pi }{4} = \frac{\pi }{4} + k2\pi \\2x - \frac{\pi }{4} =  - \frac{\pi }{4} + k2\pi \end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{4} + k\pi \\x = k\pi \end{array} \right.{\rm{, }}k \in \mathbb{Z}\)

Vậy nghiệm của (5) là \(x = k\pi \), \(x = \frac{\pi }{4} + k\pi \)\(\left( {k \in \mathbb{Z}} \right)\).

b. \({\sin ^4}x + {\cos ^4}x = 2\sin x\cos x - \frac{1}{2}{\cos ^2}2x\)

\( \Leftrightarrow 1 - 2{\sin ^2}x{\cos ^2}x = \sin 2x - \frac{1}{2}\left( {1 - {{\sin }^2}2x} \right)\)

\( \Leftrightarrow 1 - \frac{{{{\sin }^2}2x}}{2} = \sin 2x - \frac{1}{2}\left( {1 - {{\sin }^2}2x} \right)\)

\( \Leftrightarrow {\sin ^2}2x + 2\sin 2x - 3 = 0\)

Đặt \(t = \sin 2x,t \in \left[ { - 1;1} \right],\) Bất phương trình trở thành:

\({t^2} - 2t - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t =  - 3\,(loai)\end{array} \right.\)

Với \(\sin 2x = 1 \Leftrightarrow 2x = \frac{\pi }{2} + k2\pi  \Leftrightarrow x = \frac{\pi }{4} + k\pi ,k \in \mathbb{Z}\)

Vậy nghiệm của (3) là \(x = \frac{\pi }{4} + k\pi \)\(\left( {k \in \mathbb{Z}} \right)\).

c. \(\tan x + \frac{{\cos x}}{{1 + \sin x}} = 1\)

Điều kiện: \(\left\{ \begin{array}{l}\cos x \ne 0\\\sin x \ne  - 1\end{array} \right. \Leftrightarrow x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)

Khi đó (1)\( \Leftrightarrow \frac{{\sin x}}{{\cos x}} + \frac{{\cos x}}{{1 + \sin x}} = 1\)

\(\begin{array}{l} \Leftrightarrow \sin x\left( {1 + \sin x} \right) + {\cos ^2}x = \cos x\left( {1 + \sin x} \right)\\ \Leftrightarrow \sin x + 1 = \cos x\left( {1 + \sin x} \right)\end{array}\)

\( \Leftrightarrow \left( {\sin x + 1} \right)\left( {\cos x - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x =  - 1\\\cos x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x =  - \frac{\pi }{2} + k\pi \\x = k2\pi \end{array} \right.,k \in \mathbb{Z}\)

So sánh với điều kiện (*) ta được nghiệm của (1) là \(x = k2\pi \) \(\left( {k \in \mathbb{Z}} \right)\).

d. \(\cot x = \tan x + \frac{{2\cos 4x}}{{\sin 2x}}\)

Điều kiện: \(\sin 2x \ne 0 \Leftrightarrow \cos 2x \ne  \pm 1\) (*)

Khi đó (2)\( \Leftrightarrow \frac{{\cos x}}{{\sin x}} - \frac{{\sin x}}{{\cos x}} = \frac{{\cos 4x}}{{\sin x\cos x}}\)\( \Leftrightarrow {\cos ^2}x - {\sin ^2}x = \cos 4x\)

\( \Leftrightarrow \cos 2x = \cos 4x \Leftrightarrow 2{\cos ^2}2x - \cos 2x - 1 = 0\)

Đặt: \(t = \cos 2x,t \in \left( { - 1;1} \right)\)

Bất phương trình trở thành: \(2{t^2} - t - 1 = 0 \Leftrightarrow  \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = 1\,(loai){\rm{   }}}\\{t =  - \frac{1}{2}}\end{array}} \right.\)

Với \(\cos 2x =  - \frac{1}{2} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x = \frac{{2\pi }}{3} + k2\pi }\\{2x =  - \frac{{2\pi }}{3} + k2\pi }\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{\pi }{3} + k\pi }\\{x =  - \frac{\pi }{3} + k\pi }\end{array}} \right.,k \in \mathbb{Z}\)

Vậy nghiệm của (2) là \(x = \frac{\pi }{3} + k\pi \), \(x =  - \frac{\pi }{3} + k\pi \) \(\left( {k \in \mathbb{Z}} \right)\).

Ở nội dung bài Ôn tập Chương 1 đã giúp các em có các nhìn tổng quát về nội dung của chương 1 Toán 11, giúp các em tổng hợp các công thức về lượng giác để áp dụng giải các bài toán về lượng giác. 

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 11 Cánh Diều Chương 1 Ứng dụng hàm số lượng giác để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Hãy tìm mệnh đề đúng trong các mệnh đề dưới đây?

  • A. Hàm số y = sinx đồng biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\pi  + k2\pi } \right)\), và nghịch biến trên mỗi khoảng \(\left( {\pi  + k2\pi ;k2\pi } \right)\) với \(k \in Z\).
  • B. Hàm số y = sinx đồng biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{{ - \pi }}{2} + k2\pi ;k2\pi } \right)\) với \(k \in Z\).
  • C. Hàm số y = sinx đồng biến trên mỗi khoảng \(\left( {\frac{{ - 3\pi }}{2} + k2\pi ;\frac{{5\pi }}{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) với \(k \in Z\).
  • D. Hàm số y = sinx đồng biến trên mỗi khoảng \(\left( {\frac{{ - \pi }}{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\).

• Câu 2:

  Phương trình nào tương đương với phương trình \(3{{\sin }^{2}}x={{\cos }^{2}}x\) trong các phương trình dưới đây?

  • A. \(\sin x=\frac{1}{2}.\)      
  • B. \(\cos x=\frac{\sqrt{3}}{2}.\)
  • C. \({{\sin }^{2}}x=\frac{3}{4}.\)
  • D. \({{\cot }^{2}}x=3.\)

• Câu 3:

  Biến đổi phương trình \(\cos 3x-\sin x=\sqrt{3}\left( \cos x-\sin 3x \right)\) về dạng \(\sin \left( ax+b \right)=\sin \left( cx+d \right)\) với b, d thuộc khoảng \(\left( -\frac{\pi }{2};\frac{\pi }{2} \right)\). Tính b+d?                            

  • A. \(b+d=\frac{\pi }{12}.\) 
  • B. \(b+d=\frac{\pi }{4}.\)          
  • C. \(b+d=-\frac{\pi }{3}.\) 
  • D. \(b+d=\frac{\pi }{2}.\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 11 Cánh Diều Chương 1 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Giải tích 11 Cơ bản và Nâng cao.

Giải Bài 1 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 2 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 3 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 4 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 5 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 6 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 7 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 8 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 9 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 10 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 11 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 12 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 13 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Giải Bài 14 trang 41 SGK Toán 11 Cánh Diều tập 1 - CD

Bài tập 63 trang 31 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 64 trang 31 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 65 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 66 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 67 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 68 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 69 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 70 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 71 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 72 trang 32 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 73 trang 33 SBT Toán 11 Tập 1 Cánh diều - CD

Bài tập 74 trang 33 SBT Toán 11 Tập 1 Cánh diều - CD

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HỌC247 sẽ sớm trả lời cho các em.