Bài tập 74 trang 33 SBT Toán 11 Tập 1 Cánh diều
Một chất điểm chuyển động đều theo chiều ngược chiều kim đồng hồ trên đường tròn bán kính 5 cm. Khoảng cách \(h\) (cm) từ chất điểm đến trục hoành được tính theo công thức \(h = \left| y \right|\), trong đó \(y = a\sin \left( {\frac{\pi }{5}t} \right)\), với \(t\) là thời gian chuyển động của chất điểm tính bằng giây \(\left( {t \ge 0} \right)\) và chất điểm bắt đầu chuyển động từ vị trí \(A\) (Xem hình dưới)
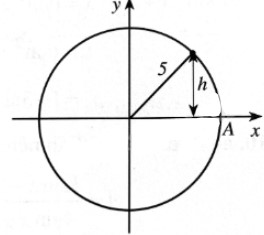
a) Chất điểm chuyển động một vòng hết bao nhiêu giây?
b) Tìm giá trị của \(a\).
c) Tìm thời điểm sao cho chất điểm ở vị trí có \(h = 2,5\) cm và nằm phía dưới trục hoành trong một vòng quay đầu tiên.
Hướng dẫn giải chi tiết Bài tập 74
a) Thời gian chất điểm chuyển động một vòng là chu kì của chất điểm đó.
Xét \(t = 0 \Rightarrow h = 0\), ta thấy chất điểm ở vị trí \(A\).
Ta cần tìm thời gian gần nhất kể từ thời điểm \(t = 0\) (giây), chất điểm lại quay về vị trí \(A\).
Xét \(h = 0 \Leftrightarrow y = 0 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = 0 \Leftrightarrow t = 5k ~\left( {k \in \mathbb{Z}} \right)\)
Với \(k = 1\), ta thấy chất điểm chuyển động được nửa vòng tròn.
Với \(k = 2\), ta thấy chất điểm chuyển động được một vòng tròn, và quay về vị trí \(A\).
Do vậy, thời gian chất điểm chuyển động một vòng là 10 giây.
b) Do thời gian chất điểm chuyển động một vòng là 10 giây, nên sau 2,5 giây chất điểm chuyển động được một phần tư vòng tròn theo chiều dương.
Như vậy tại \(t = 2,5\) ta có:
\(y = \left| y \right| = h = 5 \Leftrightarrow a\sin \left( {\frac{\pi }{5}.\frac{5}{2}} \right) = 5 \Leftrightarrow a\sin \left( {\frac{\pi }{2}} \right) = 5 \Leftrightarrow a = 5\).
\( \Rightarrow y = 5\sin \left( {\frac{\pi }{5}t} \right)\)
c) Ta cần tìm \(t\) để \(h = 2,5\)cm và ở dưới trục hoành nên \(y = - 2,5\).
\(5\sin \left( {\frac{\pi }{5}t} \right) = - 2,5 \Leftrightarrow \sin \left( {\frac{\pi }{5}t} \right) = - \frac{1}{2}\)
Ta thấy \(\sin \frac{{ - \pi }}{6} = - \frac{1}{2}\), phương trình ở trên tương đương với:
\(\sin \left( {\frac{\pi }{5}t} \right) = \sin \frac{{ - \pi }}{6}\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{5}t = - \frac{\pi }{6} + k2\pi \\\frac{\pi }{5}t = \pi + \frac{\pi }{6} + k2\pi \end{array} \right. \\\Leftrightarrow \left[ \begin{array}{l}t = \frac{{ - 5 + 60k}}{6}\\t = \frac{{35 + 60k}}{6}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\)
Vì ta chỉ xét vòng quay đầu tiên, nên \(0 \le t \le 10\).
Do đó \(t = \frac{{35}}{6}\), \(t = \frac{{55}}{6}\)
Vậy tại thời điểm \(t = \frac{{35}}{6}\) giây, \(t = \frac{{55}}{6}\) giây, chất điểm cách trục hoành 2,5 cm và nằm ở dưới trục hoành.
-- Mod Toán 11 HỌC247
Bài tập SGK khác
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


