Giải bài 2 trang 102 SGK Toán 10 Chân trời sáng tạo tập 1
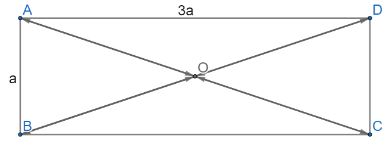
Cho hình chữ nhật ABCD có O là giao điểm của hai đường chéo và AB = a, BC = 3a.
a) Tính độ dài các vectơ \(\overrightarrow {AC} ,\overrightarrow {BD} \)
b) Tìm trong hình ảnh vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\)
Hướng dẫn giải chi tiết Bài 2
Phương pháp giải
a) Bước 1: Tính độ dài AC, BD
Bước 2: Tính độ dài vectơ \(\left| {\overrightarrow {AB} } \right| = AB\)
b) Bước 1: Tìm các đoạn thẳng có độ dài là \(\frac{{a\sqrt {10} }}{2}\)
Bước 2: Từ các đoạn thẳng trên xác định các vecto cùng phương (giá song song hoặc trùng nhau) nhưng ngược hướng.
Lời giải chi tiết
a) Ta có:
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {{\left( {3a} \right)}^2}} = a\sqrt {10} \)
+) \(\left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10} \)
+) \(\left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10} \)
b) O là giao điểm của hai đường chéo nên ta có:
\(AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}\)
Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng
Suy ra các cặp vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\) là:
\(\overrightarrow {OA} \) và \(\overrightarrow {OC} \); \(\overrightarrow {AO} \) và \(\overrightarrow {CO} \); \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \); \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 1 trang 102 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 102 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 102 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 11 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 12 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Trong mặt phẳng tọa độ \(Oxy\), cho biết khẳng định sau đúng hay sai: Vecto \(\overrightarrow a \) có hoành độ bằng 0 thì cùng phương với \(\overrightarrow j. \)
bởi Lê Minh Bảo Bảo
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời