Giải bài 8 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1
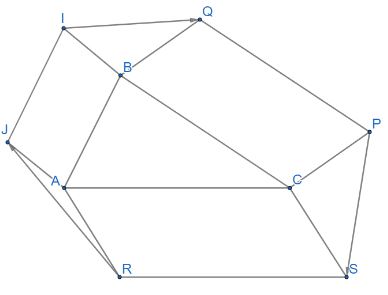
Cho tam giác ABC. Bên ngoài tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng \(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 \).
Hướng dẫn giải chi tiết Bài 8
Phương pháp giải
Bước 1: Sử dụng quy tắc ba điểm \(\overrightarrow {AB} = \overrightarrow {AO} + \overrightarrow {OB} \)
Bước 2: Xác định các cặp vectơ đối nhau từ các hình bình hành \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là hai vectơ đối nhau với ABCD là hình bình hành
Bước 3: Sử dụng tính chất của vectơ đối \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) là hai vectơ đối nhau thì\(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow 0 \)
Lời giải chi tiết
\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)\)
\( = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0 + \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \)\(\)(đpcm)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 6 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 11 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 12 trang 103 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 101 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 102 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 103 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Cho tam giác \(OAB\). Gọi \(M\) và \(N\) lần lượt là trung điểm của \(OA\) và \(OB\). Hãy tìm các số \(m, n\) sao cho: \(\overrightarrow {OM} = m\overrightarrow {OA} + n\overrightarrow {OB} \).
bởi Lê Viết Khánh
 05/09/2022
Theo dõi (0) 1 Trả lời
05/09/2022
Theo dõi (0) 1 Trả lời